在大样本研究中，例如经济学研究，流行病学研究，或是基因组研究中，要确定一个变量对另一个变量的影响因素的大小，就要利用统计学方法对其进行分析找到因果关系。
然而，在这些研究中，因素太多，导致其中的因果关系之间的关联非常复杂。孟德尔随机化就提供了这样一种方式，利用科学化的流程来确定大量因素之间的因果关系。
举个例子，肺癌的相关因素有很多，例如是否抽烟，是否有基因缺陷，环境污染，生活方式等。那么如何确定肺癌和这些因素的相关性大小，就要使用孟德尔随机化的方式。
名词来源
来自 孟德尔随机化系列之一：基础概念 Mendelian randomization I – GWASLab – GWAS实验室 作者的理解，孟德尔随机化的名字来自于“孟德尔第二定律”和“随机对照试验”。
定义变量
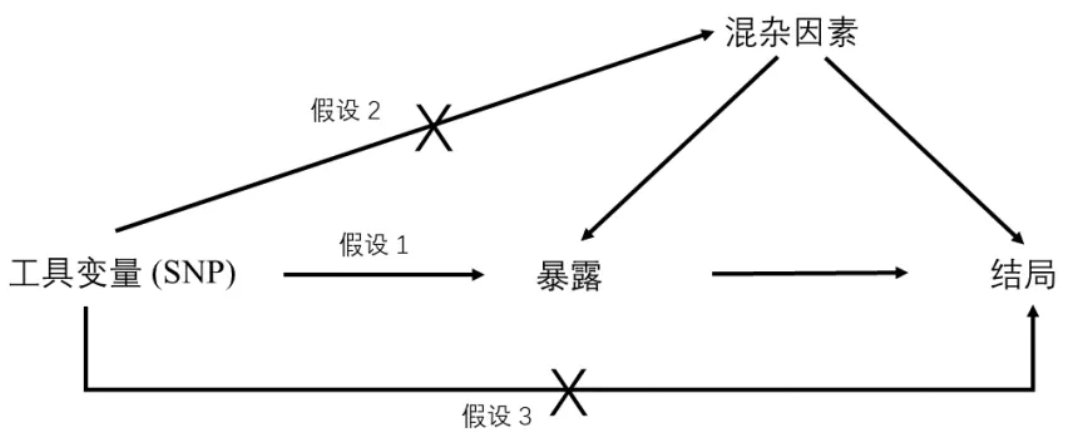研究中将不同的影响因素分为四种不同的变量
- 自变量（暴露因素）：标记为 X
- 目标变量（结局）：标记为 Y
- 混淆变量（混杂因素）：标记为 U
- 工具变量（IV）：标记为 Z 在基因分析中 Z 可以是一个影响因素，例如一个基因，X 可以是一个基因导致的性状，Y 则是最终的结果。
例如阿尔兹海默症，Y 是阿尔兹海默症，X 是一个风险因素，例如高血压，Z 是导致 X 的基因，例如和血压相关的基因。U 是混淆因素的生活方式，例如不健康的饮食，作息，抽烟等。
要应用孟德尔随机化，有两种方式分别是两阶段最小二乘法和两样本随机化。
两阶段最小二乘法
利用最小二乘法方式得到 X 和 Y 的关系，然后用相同方法得到 Y 和 Z 之间的关系。
这样一来，X 和 Y 之间是回归方法，Y 和 Z 也是。然后，便可利用回归得到的参数发现 X 和 Z 之间的相关性。
两样本随机化
因为我们要研究的因素众多，往往一个样本集中无法包含所有的变量，这时候便要采取两样本随机化的方式。
此时，在单一样本无法获取到在一个样本集中同时包含 Z、X 和 Y 。遵循以下步骤。
开始前，要选择工具变量 Z，要求是：
- 和暴露因素 X 强关联
- 和混杂因素 U 无关联
- Z 到 Y 应该是唯一的路径，没有其他的因素影响结果。
收集两种数据集：
- 第一个数据集包含遗传变异 Z 和暴露因素 X 之间的关联
- 第二个数据集包含遗传变异 Z 和结局变量 Y 之间的关联
对于以上的数据集，要保证 Z 是重叠的。然后便可以使用其他的统计学方法做进一步统计得到结果。