SVM

Support Vector Machine 支持向量机

监督学习模型，利用回归方式分类样本。

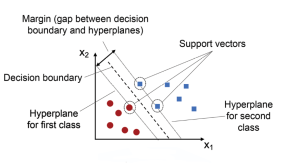
核心思想：在特征空间中构造一个线性的“超平面”，将不同类别的样本分离开来。

核心概念

超平面：即为决策边界

$$w\cdot x+b=0$$

• w 表示法向量
• b 表示偏置

支持向量：距离当前超平面最近的样本点到平面的距离。注意，样本中只有最近的样本点的距离才叫做“支持向量”，其余的样本点会被忽略。

间隔最大化：最大化支持向量到超平面的距离

优化过程

其中“间隔最大化”就是计算支持向量的最小值。

$$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}\Vert w{\Vert }^2\\ \text{s.t.}& y_i(w\cdot x_i+b)\ge 1,\forall i\end{array}$$

使用拉格朗日数乘法可将 min 的最优化问题等效为一个 max 优化问题便于计算。

$$\begin{array}{rl}\underset{\alpha }{\max }& \sum _i{\alpha }_i-\frac{1}{2}\sum _{i,j}{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j\\ \text{s.t.}& \sum _i{\alpha }_i{y}_i=0,{\alpha }_i\ge 0\end{array}$$

决策函数

$f(x)=\text{sign}(w\cdot x+b)$ 使用决策函数将样本带入计算，可以获得一个 -1/1 的值，从该值可以判断样本是否被正确分类。

核方法

很多情况下样本无法在一个线性空间中被一个超平面完美分类。这时候就可以考虑将样本映射到一个更高维的空间中，使用超平面进一步分类。

核函数，就是通过一个映射函数，将所有的样本升维，然后计算。

例如：

• 多项式核 ：$K(x,z)=(x\cdot z+c{)}^d$
• 高斯核（RBF核）：$K(x,z)=\exp (-\gamma \Vert x-z{\Vert }^2)$

其中：

• x,z 为两个不同的样本。

每个核函数对应一个特征映射函数 $\varphi (x)$。

例如当 d=2 的二阶多项式核对应的特征映射为，该特征映射的内积就是 K(x,z) 的结果：

$$\varphi (x)=[x_1^2,x_2^2,\sqrt{2}{x}_1{x}_2,\sqrt{2c}{x}_1,\sqrt{2c}{x}_2,c]$$

决策函数可以更改为：

$$f(x)=\text{sign}\left(\sum _i{\alpha }_i{y}_{i}K(x_i,x)+b\right)$$