Neural Networks
属于机器学习算法的一种。参考神经科学中神经元组织的方式,形成一个参数和数据流动的计算网络。
神经网络的强项在于模式识别,即为,在海量的数据中找寻规律,并将识别的规律总结输出。
计算过程
神经网络的本质是一个“计算图”,由节点和边构成。节点表示了数据的一个计算过程,可以用一个公式表示,边表示数据的流向。
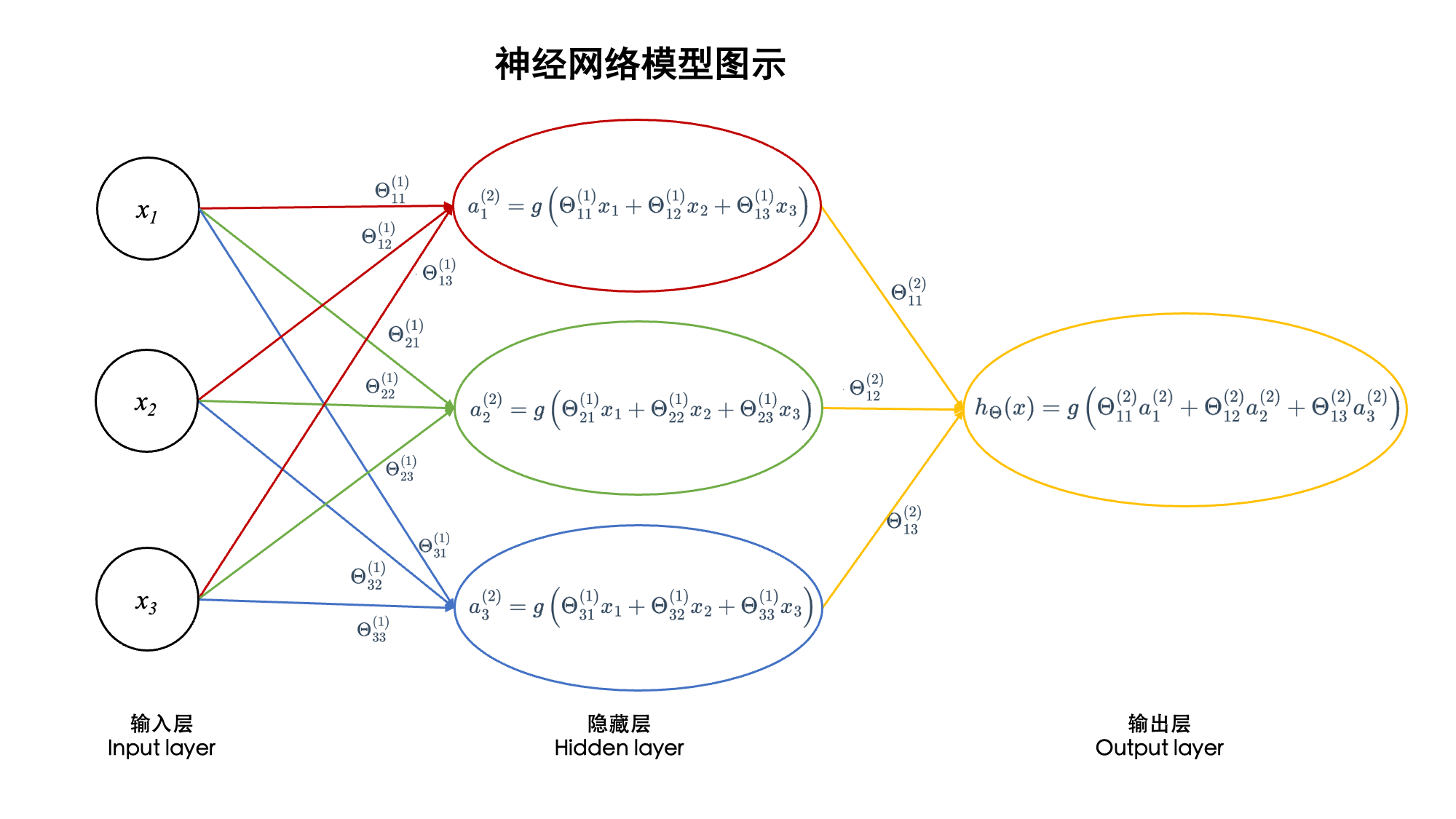
中间可以有一个或数个隐藏层,每一个隐藏层代表了一次数据处理。
数据(参数)在网络中流动,从输入层经过计算到输出层,输入层一般为原始数据,输出层为计算得到的结果。例如要在图片中识别猫,输入可以为猫的图片,那么输出结果即为“图片中是否包含有猫”。
数据结构
神经网络中一般使用矩阵作为参数的存储数据结构,使用线性代数法则计算,一般来讲有几种矩阵
- 输入数据矩阵,表现为数据和特征数值的矩阵。一般一行为一条数据,每列表示不同的特征数据
- 参数矩阵,神经网络的每一层可用一个参数矩阵表示。参数的输入为前一层或者输入层传入的矩阵。经过一个矩阵乘法和一个非线性函数的过滤计算(一般是用sigmoid或者ReLU)得到一个结果,结果也表示为矩阵。
- 输出矩阵,数据可以是矩阵也可以是一个向量,在图像识别的任务中,如果每个数据仅有单一输出,那么输出为一个向量,每一行对应了一个输入数据,行对应的一个标量表示输出的结果。
神经网络的数据结构和图的结构是一致的,图可以用矩阵来表示和计算,神经网络也是一样。
算法
神经网络中的算法主要包含两个,前向传播和反向传播。
前向传播(推理/预测过程)
前向传播对应推理和预测过程。即为给一个输入,然后将输入数据在神经网络中从前向后传输,经过每一层的参数计算,最终获得输出结果。
前向传播中的每一个中间层的计算可以表示为
其中 W 表示参数矩阵,X 表示前一层进入的数据,b 表示在该层中加入的偏移量,Z 表示矩阵乘法后计算得到的结果,A 表示经过非线性函数后得到的结果。A 将被送入下一层计算。
当计算到最后一层时,会使用一个输出函数,例如 softmax 得到最终结果。
反向传播(参数更新,训练过程)
反向传播对应参数更新过程。反向传播发生在前向传播之后,在前向传播获得结果之后,反向传播用微积分求导方式更新模型中的参数。
反向传播对应机器学习中的“监督学习”,即在已知结果的情况下,用前向传播得到模型的预测结果,计算结果和真实值之间的差值,用差值来计算模型中的各个参数。
先求 Z 的微分,从真实值和模型的预测值计算差值,然后计算参数矩阵 W 的梯度,最后计算 b 的梯度,最终用梯度下降算法更新参数 W 和 b。
从直觉感受上来看,就是将模型在前向传播中的输出与真实值做比较,根据这个比较出来的差值多少,利用求导方式从后往前更新模型中的参数,将模型参数与最终的结果拟合在一起。
缩放定律
时间上的缩放定律,神经网络在时间上的缩放定律体现为训练的时间。训练时间的越长,模型的拟合效果越好。但是过长的训练时间会导致模型出现过拟合问题。
空间上的缩放定律则是更为明确的。表现为训练数据量越大,模型的参数越多,获得的训练效果越好。
然而,神经网络可以有很多种不同的形式,不同的形式在不同任务中的表现可以很不一样。例如CNN擅长处理图片,RNN擅长处理时序数据,例如对语言的建模。