用一条直线拟合有线性关系的数据,使得这个直线和真实数据之间的误差最小。
假设我们有一堆数据,这些数据之间有线性关系,我们需要用一个线性函数来描述这种关系,利用最小二乘法可以保证获得的线性函数和真实值之间的误差尽量小。是一种回归方法。
不仅仅是线性回归方法,非线性回归也适用。
计算过程
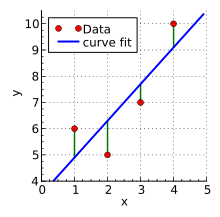
目标是寻找一个线性函数(蓝线),使得红点到蓝线之间的距离最小
使得
其中 和 b 是模型的参数,所得的直线为拟合后的结果。
优势与劣势
优势是计算简便,公式简单,符合数学的简单美,也是最基础的回归分析方法。
劣势也很明显,主要有三个:
- 无法处理数据稀疏的问题,强行对稀疏数据处理可能会获得奇怪的结果
- 对独立同分布的假设:最小二乘法假设所有的变量都是独立同分布,而这和现实情况不一定相符。
- 解释性矛盾:最小二乘法取得的模型,因为获得的是统计性结论,对模型的解释性可能不是最强的。
类比到 损失函数
损失函数是机器学习领域的重要概念。如果利用最小二乘法计算损失函数,那么获得的函数为:
以上公式,和均方误差很类似类似,注意到其中都是差值的平方和。m 为总样本数量
计算复杂度
根据 线性回归之最小二乘法 - 李一二 - 博客园 ,了解到计算复杂度为 ,其中 n 为样本数量,复杂度比较高。如果只用单纯的最小二乘法的话,一般在工程上这个计算复杂度是不可接受的,需要用优化方法进一步减小复杂度。