Turing Machine,计算机的数学理论表示。
图灵机模型由艾伦·图灵提出,伟大的数学家,计算机科学家。
图灵机可解决的问题,就是计算机可解决的问题,也即为计算的极限。
概念
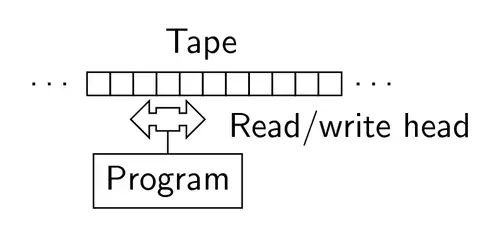
来自吴军在《计算之魂》这本书里对图灵机的基本概念总结为四条定义:
- 无限长的纸带,带编号的格子里记录符号或者数字
- 读写头,可以改变当前位置的符号和数字
- 规则表,根据当前状态知道下一步的操作
- 寄存器,记录当前图灵机的状态,这个状态必须是有限的
然后,他将图灵机模型的意义总结为三条:
- 计算问题被分为了两类,分别是有限步骤的计算和无法在有限步骤完成的计算
- 提出了计算机的一个基本理论架构,由存储地址,计算机的状态,规则表,读写头。
- 将数学问题和机械运动对应(当然现在是电子运动了,不过也是一个道理)
当今的计算机和图灵机
图灵机为什么伟大,是因为这个理论模型是现在所有计算机的理论模型。可以说,不论当今计算机的 CPU ,内存还是硬盘,都遵循了这个架构。CPU 中有寄存器,有虚拟的读写头,内存和硬盘中有存储地址,而我们编写的计算机程序,其实就是“规则表”。
而在机器学习场景中,规则表就是模型,状态就是模型在推理时的参数变化,存储及其地址就是数据集,读写头则代表了对数据的操作,以及输入和输出。
所以,计算机发展到现在,其底层的理论框架一直没有变过。万变不离其宗,这就是计算机领域的“宗”。
可计算理论
如果一个问题是图灵机可以解决的,那我们就称之为“可计算问题”。一般来说,我们在高中和大学中学习的数学问题都是可计算问题,例如:
- 对某一个函数求导
- 判断正整数n是否是指数
- 判断一个逻辑蕴含问题,求其逆否命题
而生活中的许多问题,都不是可计算问题,例如:
- 今天出门是否要开车?
- 晚上吃什么?
- 世界上有神存在吗?
一般我们能遇到的逻辑推断问题,数学问题,还有证明问题,基本都是可计算的。数学上,有专门的一个分支研究可计算性问题,叫作“可计算理论”
停机问题
提到图灵机,就一定会提到停机问题。停机问题是一类典型的不可计算问题。是由图灵在1936年首次提出的。
停机问题可以总结为:
假设一个图灵机,它是否可以在开始计算之前就知道程序什么时候会停下来?
另一种表述方式是:
是否可以判断一个程序是否可以在有限的时间内结束运行?
用程序员的话说就是:当我写好一个程序之后,我是否可以判断,在任意输入的情况下,这个程序会什么时候结束(中途出错或者完成)?
然而,图灵却证明了,停机问题属于“不可判定问题”,即我们无法判断会程序在什么时候结束。对于程序员这不是一个好消息,因为我们永远无法知道自己的程序什么时候会出错。
关于此,我有一个感想。也许人工智能永远无法替代人类调试程序,因为停机问题是无法计算的。
关于停机问题及其利用反证法的证明,可移步:计算的极限(二):自我指涉与不可判定 | fwjmath的相空间
图灵完备性
通常,图灵完备性描述的是编程语言的性质,满足图灵完备性的语言可以实现所有图灵机的操作,进而可以处理所有的“可计算”问题。
我们经常接触的编程语言,例如 Python,Java,C,汇编都是图灵完备语言。它们都有共同点,例如都有流程控制(判断语句,循环语句等),变量声明等。这些共同的特性决定了他们的图灵完备性。另外一些语言,例如最原始的 SQL 和 HTML 语言,它们不是图灵完备的。在我的经验里,这些语言总是“缺乏”了一些功能,无法完成所有的工作。当然 SQL 在支持“存储过程”之后,已经成为图灵完备语言。
至于这些编程语言的图灵完备性在数学上的证明,这一点我还需要继续研究。
C++ 或者 Java 属于高级语言,其高级语言的特性,例如类,错误处理,函数式编程等,其实都是在流程控制的基础上整理和演化而来,并不是基础语言的特性。
有一种特殊的语言 BrainFuck 支持以图灵机非常原始的方式编程,BrainFuck 是图灵完备的。它总共有八种原始指令,可以整理为三类:
- 指针移动类指令:控制图灵机指针的位置,直接移动和按照标记跳转
- 数据操作指令:控制当前指针下面数据的加减
- IO指令:从终端读取数据或输出数据到终端
关于 BrainFuck 语言,看起来就是,以下代码向终端输出“HelloWorld”:
++++++++[>++++[>++>+++>+++>+<<<<-]>+>+>->>+[<]<-]>>.>--.+++++++..+++.>>.<-.<.+++.------.--------.>>+.>++.该示例来自于:Brainfuck - Wikipedia
特殊的图灵机
通用图灵机
通用图灵机和谕示机都是一种特殊的图灵机。
通用图灵机是一种“模拟图灵机的图灵机”,可谓是图灵机的“套娃”。
我认为通用图灵机其实就是我们常用的“虚拟机”。虚拟机里面可以运行其他的操作系统,而通用图灵机也是一样,他可以模拟其他的图灵机。图灵机可以分很多种,不同的图灵机可以有不同的结构和不同的运行规则,但是他们同样都是图灵机。不论哪种图灵机,他们在数学上都是等价的,所有的图灵机都可以相互表示。
谕示机
我在这篇文章中见到了“谕示机”这个概念:计算的极限(十):无限绵延的层级 | fwjmath的相空间
谕示机则更有意思,一般用于数学假设和推导。谕示机除了图灵机的功能之外,还有一张特殊的“表”,这个表里面有各种各样不可计算问题的答案。假设,表里关于“今天晚上吃什么”这个问题有一个答案,假设是“大螃蟹”。
谕示机可以通过查找规则表,解决不可计算的问题。但是尽管如此,谕示机仍然无法逃出可计算问题的范畴,因为查表操作的本质其实还是计算。
不确定性图灵机
在计算复杂度理论中,涉及到不确定性图灵机。在经典图灵机中,图灵机的读写头只有一个,意味着它一次只能处理一个指令。而不确定性图灵机可以在一个步骤内同时计算很多种可能性,然后用分治方法将返回值合并,最终取得结果。
这个过程就有点像现代计算机中的多核计算机,可以并行计算并同时返回结果。不过不确定性图灵机是在理论上可以一下子同时计算所有的可能性,不受核心数量的限制,而多核计算机的 CPU 资源数量是固定的。
对编程实践的影响
对于了解图灵机的原理以后,对编程实践有什么启发,我有三个总结:分别是编码思维,封装思维和数据一致性。
编码思维
这个最简单,就是图灵机只会“认识”已经通过规则表指定的字符集。例如,我们可以规定图灵机认识 0 和 1,也可以教它认识 0-9,a-z 这样的字符。
在规定的过程中,同时我们已经完成了对数据的编码。计算机能做的,其实就是对信息数据的计算,而编码则是计算的第一步。
封装思维
在主流的高级编程语言中,例如 Java,会用不同的方式封装代码块。例如“类”就是对相似功能代码的逻辑封装,同时类又可以被拓展、继承,这就是对封装的拓展。
而在另一些语言中则使用了函数式编程的方法,例如 JavaScript。虽然其也有“类”,但是它的底层逻辑更像是“函数”。其中类的实现在底层也是函数。JavaScript 的函数可以返回一个值也可以返回一个对象。这里的函数就是一种对代码的封装。
有了函数的封装,我们就可以完成更多高级的操作。例如在闭包把变量通过函数封装在一个作用域内(JS),还可以利用链运算符操作同一个对象(JS),或者用函数套函数做成装饰器(Python)。
封装之下,编程也可以玩出花。
数据一致性和内存安全
先说数据一致性。数据一致性指的是输入输出和代码对计算机来说是一样的,都是数据。“程序”对应的是图灵机的规则表,也是我们每天写的代码。“输入输出”对应就是纸带上的数据。一个字符串,可以是程序也可是输入输出数据,也就是说,我们写的程序在特定情况下可以是输入输出,输入输出也可以变为程序。
为什么写代码的时候要讲究内存安全?因为不安全的内存溢出等问题会让计算机混淆内存里待处理的数据与程序。这种情况下,计算机可能将本应该当作输入输出的数据当作程序来执行,这就成了安全漏洞(一般是注入),黑客可以用这样的方法来上传自己的代码让目标计算机执行。
内存安全就是保证该被当作程序的数据一定是程序,该被当作输入的就一定是输入,两者不被混淆。