用于描述单个算法的复杂性,即为:
- 算法需要的计算时间
- 运行算法所需的内存空间
计算复杂度理论研究的是算法的复杂性。一个可计算问题,在利用算法解决时,究竟需要多少资源?如果所需资源过多,一个问题就会在工程上不可解,那么这样一来,原本可计算的问题也就变得不可计算了。
判定性问题
一个算法问题,可以分成两类:
- 判定性问题:是不是存在解,回答是“是”或者“否”。
- 搜索性问题(求解问题):具体的解是什么,回答是一个解,或者无解
判定性问题一般是搜索性问题的前置条件,如果搜索性问题可以得到一个解,那么这个问题就一定是可判定的。
例如,一个判定性问题可以是“判断整数 1 是否在自然数中?”,而搜索性问题则更进一步,得到答案:整数 1 是在自然数中的第二个位置。其中,“第二个位置”就是这个问题的解。
对于可计算理论来讲,只研究判定性问题。
算法分析:大 O 表示
由高德纳提出的“大O表示法”是一种算法分析方法,目的是忽略计算模型中的常数因子,而关注对算法影响最大的指数部分。
其本质是“抓大放小”。
例如,n 表示输入的长度,T(n) 表示算法运行的时间长度。如果算法可在常熟时间内运行完毕,算法的时间复杂度即为 O(n)
计算问题的集合
不同的计算问题有不同的复杂性,根据问题的等价关系,可以将问题按照复杂度打包成集合。
- P 问题:在“确定性图灵机”上,所需要的计算时间不超过一个确定的多项式
- NP 问题:在“不确定性图灵机”上,所需要的计算时间不超过一个确定的多项式
- L 问题:n 为输入长度,在确定性图灵机上所需空间不超过 O(logn) 算法问题的集合。一般认为这样的算法是比较快的
其中两个重要概念:
- 确定性图灵机和不确定性图灵机:确定性图灵机每次只能做一次计算,不确定性图灵机每次可以对不同的分支同时计算,可以对每个步骤中的分支同时计算。用现代计算机来类比,确定性图灵机类似于单核计算机,而不确定性图灵机类似于多核计算机,能够并行计算。参见:不确定性图灵机
- 多项式计算时间:算法执行的步骤总数是一个多项式,例如 而不存在例如 这样的因子。
一般认为『有效算法』即为多项式步骤的算法。
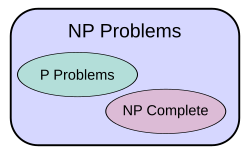
P = NP ?
P 问题和 NP 问题考虑的都是“判定性问题”。
NP 完备问题考虑的是所有 NP 问题中最难问题的集合,对于 NP完备问题,我们至今无法找到多项式步骤的算法。所以我们目前认为 。