等价,是数学上的另一个重要思想。
正是有了等价,数学问题之间才可以互相转换,也是问题解决方案相互迁移的重要前提。
在生活中,只有两个问题等价了,他们之间的才能做等效的对比。
逻辑学基础
逻辑学中,命题等价的意义是,命题之间可以相互推导,两个命题同真同假。
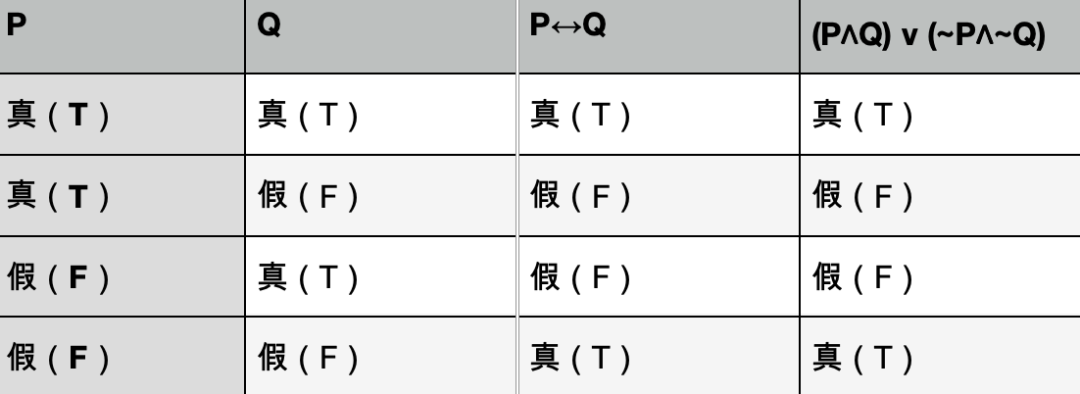
逻辑学上的等效是一切等价的基础。
等价,描述的是一种“共同”的关系,例如在谈恋爱的时候,恋人们往往会共同行动。一个人去参加一个活动,则另一个人也一起去,如果不去那么两个人都不去,这就是“等价”。
逆否命题和原命题是等价的
要注意的是,原命题和逆否命题是等价的,而和否命题与逆命题无关。原命题成立,否命题和逆命题不一定成立。
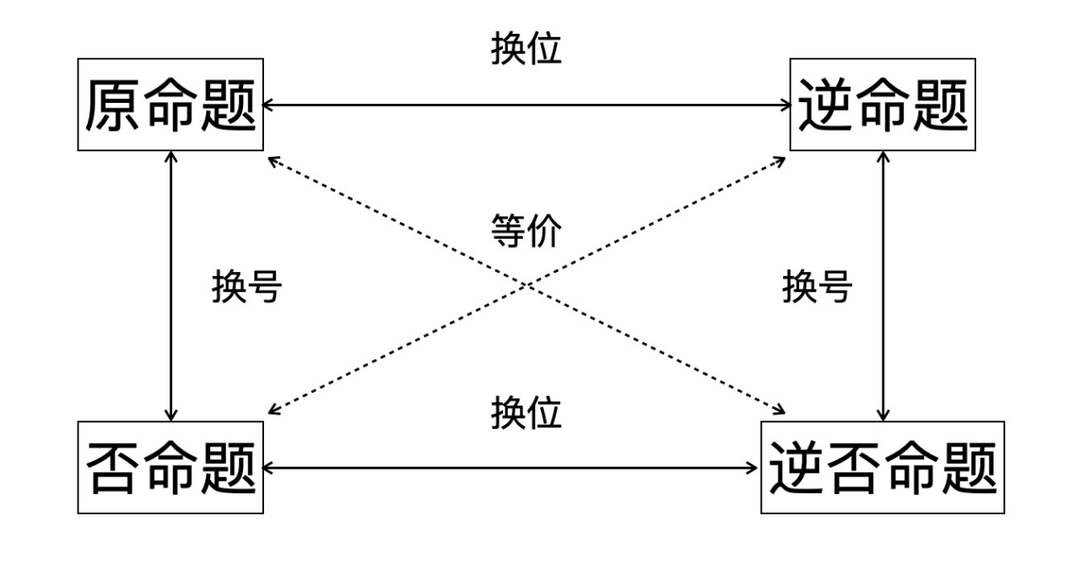
例如,原命题“只要好好学习,就能考上好大学”的等价逆否命题是“如果没考上好大学,那么就一定没好好学习”。而“不好好学习,也能考上大学”和“考上好大学,就一定好好学习了”则不是原命题的等价命题。
再比如,有一句红歌“没有共产党,就没有新中国”的逆否命题是“有了新中国,就一定有共产党”。这也符合当前的现实情况。
等价拆分
有了等价逻辑,拆分的思维才有逻辑基础。当我们需要做一个复杂项目的时候,往往没法直接做,而需要对项目作拆分,然后一步一步完成。
项目合理拆分背后的底层逻辑就是一个假设:“当所有子项目完成以后,整体项目就完成了”。
例如在做 web 开发项目时,我们先要做产品分析策划,然后是产品设计,技术设计,技术开发,软件测试。而在产品设计过程中,产品经理要对产品做合理的功能拆分,实体命名,逻辑细化才能交付开发。产品功能拆分的过程中,就是“等价拆分”的逻辑。
好的产品经理能够保证拆分出来的功能和要实现的目标功能是等价的,而若没有等价的思维,则很难保证这一点,做出来的产品就会有功能上的缺陷。
金字塔原理就是一个利用等价拆分解决问题的方法。
重构等价
在编程中,“重构”就是一个等价问题。在重构项目的时候,我们并没有改变项目的输入输出,功能逻辑,而是用了更合理的实现方法替代之前的。在这里,重构就是一个等价操作。
重构对于开发者来说是痛苦的,因为当下没有任何显性的收益。重构一般是为了更合理的代码可读性或者是项目可维护性。而不合理的重构可能会引入新的 BUG,在当下看来,重构是一个“吃力不讨好”的工作。但是在长期看,项目的重构意义重大,是避免欠技术债和扩展灾难的重要手段。
历史观:历史上的相似不等于等价
合理的知识迁移是建立在问题等价的基础上的,如果问题本身不等价,那么我们对一件事情的看法、观点、经验是无法迁移到另一件事情上的。
很多人喜欢用历史上发生的事情来理解当下发生的事。例如有人会把春秋战国时代的大国争霸类比到现在的中美竞争上。诚然大国之间的权力竞争都有一定的相似性,但是在春秋时期的国际关系中发生的事情,是在同一个文明圈内部,而当前世界的国际竞争,则是多种文明的碰撞交锋,这与中国历史上的情况完全不同,解决方案也完全不同。
要解决当下的问题,参考历史很重要,但是,更多考虑用当下的方案解决更合理。