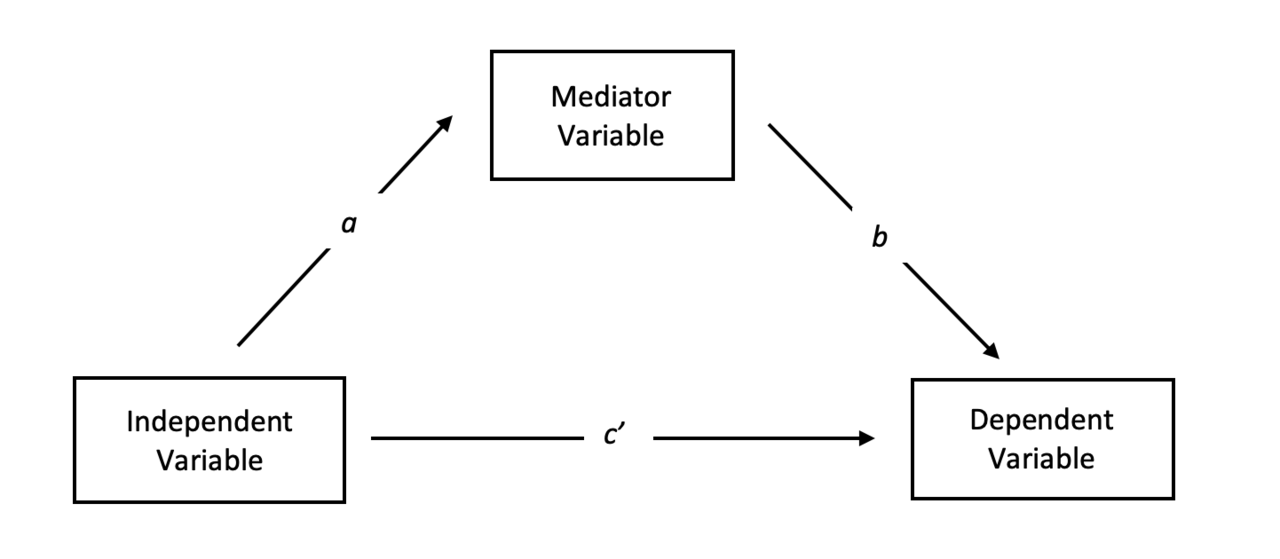
有三种变量:自变量,因变量和中间变量。自变量是引起系统变化的量。因变量是我们可见的系统结果。中间变量更多是呈现在自变量和因变量之间的桥梁过度作用的变量。
中介分析就是在判断:中间变量在自变量到因变量路径上到底有多大影响
逐步回归法
图中,我们分别检验 a、b、c’ ,可以判断是完全中介还是逐步中介。
举个例子:研究工作压力(X)如何通过睡眠质量(M)影响工作表现(Y)。
数据假设: 假设我们收集了100名员工的数据,并进行了以下回归分析:
- 总效应(c路径): 工作表现 = β₀ + c(工作压力) + e
Y = 10 - 0.5X + e
这表明工作压力每增加1个单位,工作表现平均下降0.5个单位。
- 路径a: 睡眠质量 = β₀ + a(工作压力) + e
M = 8 - 0.4X + e
工作压力每增加1个单位,睡眠质量平均下降0.4个单位。
- 路径b和c’: 工作表现 = β₀ + c’(工作压力) + b(睡眠质量) + e
Y = 8 - 0.3X + 0.5M + e
中介效应计算:
- 间接效应 = a × b = (-0.4) × (0.5) = -0.2
- 直接效应 = c’ = -0.3
- 总效应 = 直接效应 + 间接效应 = -0.3 + (-0.2) = -0.5
解释:
- 工作压力对工作表现的总影响是-0.5(总效应)
- 其中-0.3是直接影响(直接效应)
- -0.2是通过影响睡眠质量间接造成的(间接效应)
- 这说明工作压力通过两种方式影响工作表现:
- 直接降低工作表现
- 通过降低睡眠质量间接降低工作表现
中介效应比例:
- 中介效应占总效应的比例 = -0.2/-0.5 = 40%
- 这表明40%的工作压力对工作表现的影响是通过睡眠质量这个中介变量实现的
总结一下,我们先计算自变量到因变量之间的回归关系,然后引入中间变量之后,分别计算自变量到中间变量,中间变量到因变量之间的关系,最后得到的一个比例即为中介效应的显著成都。