Zhiyuan Li, Chain of Thought Empowers Transformers to Solve Inherently Serial Problems
src: 2402.12875
利用数学方式证明思维链能力的上限。
电路理论
研究者使用电路理论研究了语言模型在使用 CoT 之后的性能提升。从题目中可以看出,论文考察的问题主要是“序列问题”,即为需要按照步骤来一步步解决的问题。
分步计算
受益于 CoT 的分步计算,提升了语言模型处理问题的迭代数,可以从以下两个方面理解:
- 并行计算的结构:语言模型的并行结构决定了在计算过程中不同计算部分之间的交际较少,因为其互相之间没有数据交换所以无法互相参考。而 CoT 拓展了计算步骤,使得几个步骤之间的数据获得互相参考的机会,进而提升了模型能力。
- 步骤限制被解除:某些数学问题本身就是应该用多步骤方法处理的,不使用 CoT 的语言模型单步给出的答案往往会跳过中间步骤而不准确,CoT 解除了步骤的限制,更适合处理多步骤的问题
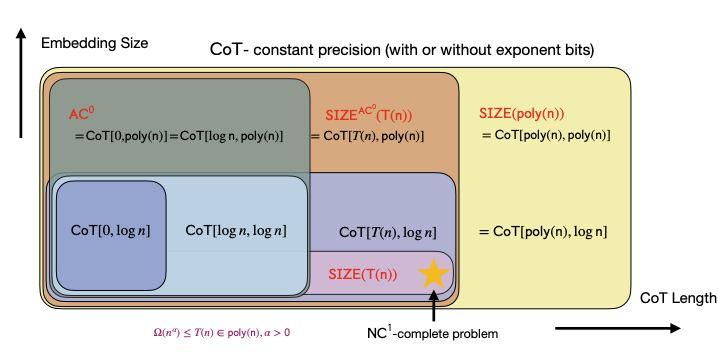
从论文中的上图可以看出。嵌入的大小和 CoT 的长度就像是空间和时间上的两个维度,维度越大,语言模型最终获得的结果也就越好。
计算复杂度的结论
使用 CoT 的语言模型解决问题的上限已经几乎包括了所有“P 问题”,即为在多项式步骤内可以解决的问题。可以看出这样的复杂度上限已经非常高了,说明 CoT 在解决问题的能力上更上一层楼。
注意到论文中使用了可计算理论和集合论来论述计算边界的问题。可以算的数学问题被打包成一个一个集合,集合内最难的问题定义了该集合的边界,随着 CoT 长度增加,更大的集合被囊括进来,表示可解决问题的边界不断扩展。