Computability Theory
别称:递归理论
可计算理论研究可计算性,如果说“一个函数或问题可以用某种算法在有限时间内解决”,那么这个问题就是可计算的。
问题分类
一个算法问题,可以分成几类:
判定问题一般是搜索性问题的前置条件,如果搜索性问题可以得到一个解,那么这个问题就一定是可判定的。
例如,一个判定性问题可以是“判断整数 1 是否在自然数中?”,而搜索性问题则更进一步,得到答案:整数 1 是在自然数中的第二个位置。其中,“第二个位置”就是这个问题的解。
对于可计算理论来讲,只研究判定性问题。
计算模型
计算模型就是用于研究可计算理论的模型,常用的计算模型有:
- 图灵机:现代计算机仍然在使用的计算理论。
- 寄存器机器:和图灵机等价。由寄存器和程序计数器来执行计算的机器,更加贴近现代计算机的底层架构。
- lambda演算:和图灵机等价。使用变元和函数来对数学做函数抽象的方式。主要方法为变量替换和带入
核心概念
可判定性:可以找到合适的算法,来判定一个问题又没有解。可判定不意味着要利用某个算法直接解决问题,而只是找到解是否存在即可。然而,有很多问题是不可判定的,也就是一个问题,我们无法知道是有解还是无解。
递归可枚举集:所有可计算函数的集合
- 递归:可计算函数用递归方法(调用自身)生成的新函数,这所有的函数组成的集合。
- 可枚举:集合中的元素可以逐个列举。
递归可枚举意味着利用递归过程,可以全部列举集合中的元素,因此,递归可枚举集就是可计算的。
递归在计算机中属于高概念,递归保证了算法在搜索时完整性。递归就像是章鱼的触手,经过层层迭代到达每一个算法可以遍历到的角落,而这些角落组成的集合就是“递归可枚举集”。我想这也是可计算理论为什么叫“递归理论“的原因。
不可计算问题(不可判定问题)
停机问题认为是可计算理论中的著名问题。
原问题表述:
使用一个算法,来判定图灵机在给定输入的情况下,最终是否会停机或者先入死循环
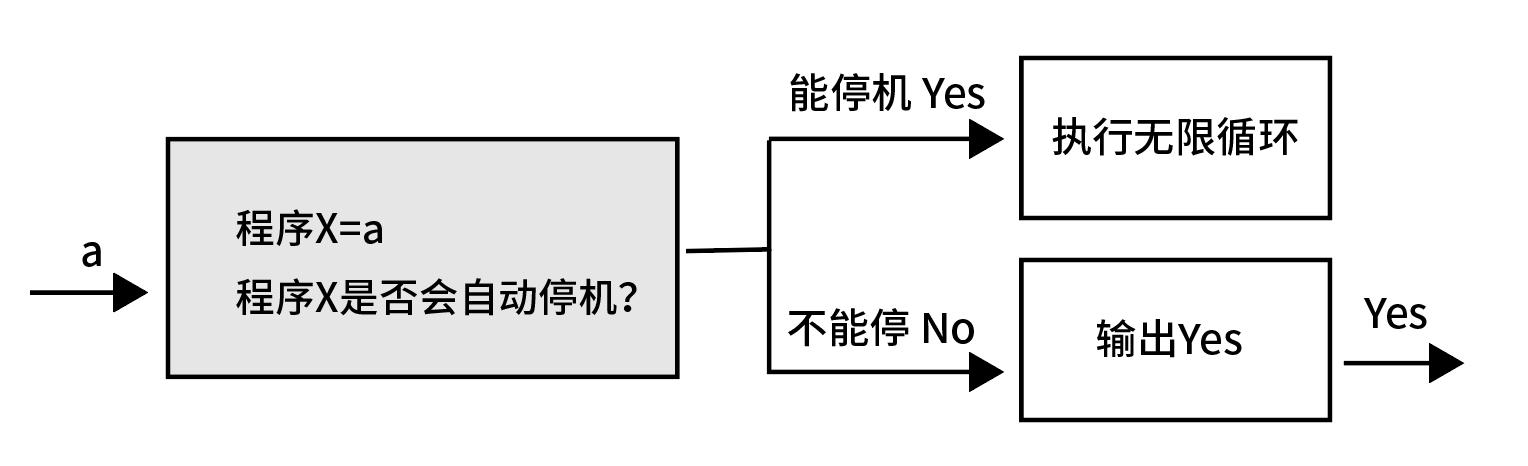
图灵利用反证法的矛盾来证明其不可计算性。图灵做了几个假设:
- 算法 P:能够判断任意程序在特定输入下是否停止运行
- 程序 Q:如果 P 输出结果为停机,那就陷入死循环,如果 P 输出结果为不停机,那就停机。
然后,程序 Q 自己运行自己。这样一来就会出现矛盾,因为无论 P 的判断如何,Q 的输出结果都相反。陷入自我指涉的矛盾:“如果 Q 停机,那么 Q 不停机;如果 Q 不停机,那么 Q 停机”,这样的矛盾无法调和。
正因为图灵证明了停机问题的不可计算性,所以大卫·希尔伯特提出的“可判定性”问题就不是可计算的,也就是说:“总有一部分问题,无法判断其是否存在解”