EM算法

Expectation Maximization Algorithm 期望最大算法。

在 MLE 的基础上，引入了一个新的隐变量 Z，表示样本在总体中的分布情况。

例如：投硬币问题中，若两个硬币试验，但是只知道投掷结果，不知道具体哪一次使用了哪个硬币。这里使用硬币的情况就是一个“隐变量”，因为我们只能从结果中推测，而无法被直接观测到。

因此，在这个问题中，有两个量需要处理：

• 参数 $\theta$ ，即为“个体”内部概率分布的情况
• 隐变量 Z，即为“个体”在试验中的分布情况

如果没有 Z，则直接可以用 MLE 估计参数。

src: 【机器学习】EM——期望最大（非常详细） - 知乎

步骤

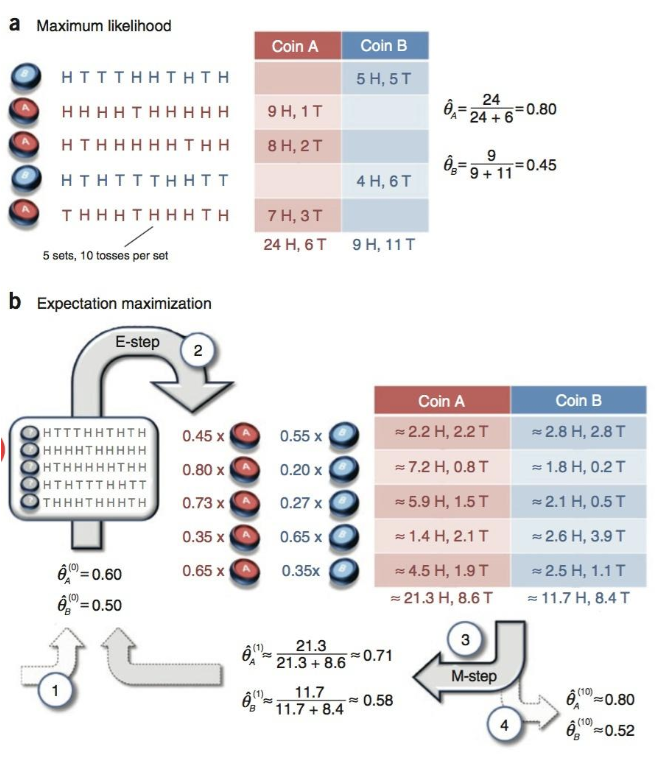
• a 为没有隐变量 Z 的情况，直接使用 MLE 即可获得估计的参数。
• b 为使用 EM 算法的情况，注意硬币编号被抹去，成为了隐变量 Z

具体步骤：

• E-step：利用参数 $\theta$，计算隐变量 Z 的分布

使用观测数据，获得隐变量 Z 的分布，对应步骤 2

• M-step：在固定隐变量之后，利用 MLE 估计参数

固定隐变量得到 Coin A 和 Coin B 对结果的贡献，然后利用 MLE 估计，对应步骤 3

理解

在 EM 算法的具体推导过程中，引入了对隐变量 Z 的分布表示 $Q_i(z)$ ，并且求和为 1： ${\sum }_z^Z{Q}_i(z)=1$

迭代过程中，不断调整参数和 Q 来逼近似然 J。

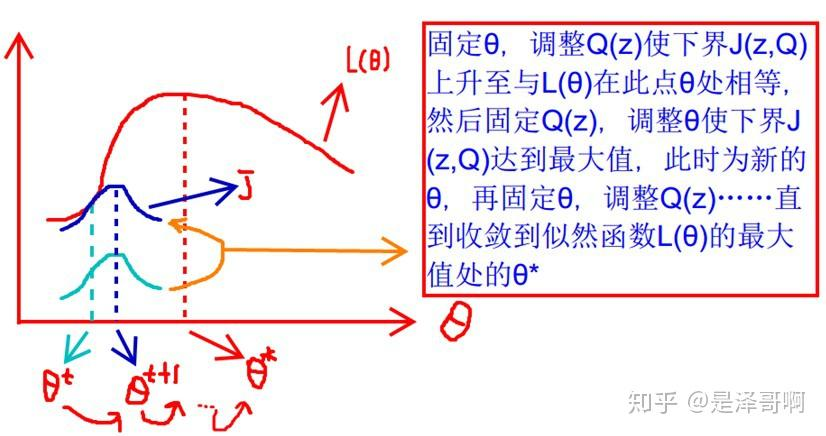
利用坐标上升法来理解，就是：

• E-step：固定参数，优化 Q
• M-step：固定 Q 优化参数，这里使用的是 MLE