HMM

Hidden Markov Model，隐马尔可夫模型

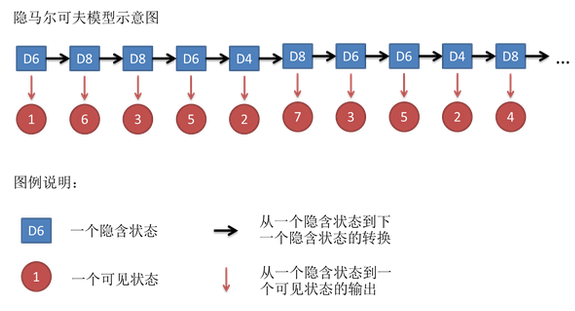
一种对时间（或状态）序列建模的模型。HMM 依赖于一阶马尔可夫假设。

HMM 假设模型有多个内部状态，各个内部状态会互相转变。每个内部状态会引出一组可观测的状态。人们仅能从可观测状态了解 HMM 的变化。

模型简述

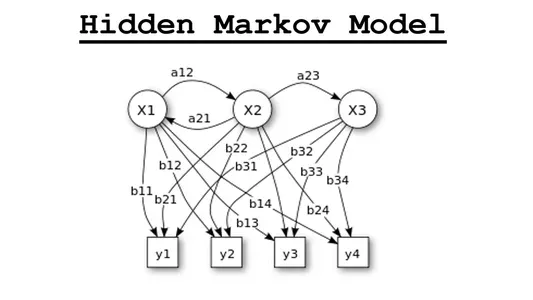
HMM 是一个图，从状态看分为两个部分：

• $Q=\left\{q_1,q_2,\dots ,q_N\right\}$ 所有可能的隐藏状态
• $V=\left\{v_1,v_2,\dots v_M\right\}$ 所有可能的可见状态

HMM 在时间上的演变，得到一个以 T 为长度的序列

• $I=\left\{i_1,i_2,\dots ,i_T\right\}$ 隐藏状态序列
• $O=\left\{o_1,o_2,\dots o_T\right\}$ 观察状态序列

• 一阶齐次马尔可夫假设- 描述状态转移：t 时刻的隐藏状态仅取决于前一个隐藏状态。

$a_{ij}=P(i_{t+1}=qj|i_t=q_i)$ 由此组成状态转移矩阵 $A={\left[a_{ij}\right]}_{N\times N}$

• 观测独立性假设 - 对于输出单元的概率假设：能观测到状态仅依赖于当前的隐藏状态

$$b_j(k)=P\left(o_t=v_k\mid i_t=q_j\right)$$

由此组成生成概率矩阵 $B={\left[b_j(k)\right]}_{N\times M}$

• 初始状态：再定义一个初始状态

$$\Pi =[\pi (i){]}_N\text{ 其中 }\pi (i)=P\left(i_1=q_i\right)$$

局限：可能不适应复杂依赖关系；需要处理数值下溢

HMM 的基本构成

• 隐藏状态和可见状态：模型的内部状态是隐藏的，可观测的数据由隐藏状态导出。
  • 隐藏状态是内部状态，无法被直接观测，表示事物的真实发展规律
  • 可见状态可被观测，但是只能从观测的数值间接了解到隐藏的内部状态
• 三部分参数：
  • 初始状态分布 $\pi$ ，初始状态概率
  • 状态转移矩阵 A，状态之间发生转换的概率，$A[i][j]$ 表示 i 到 j 的转移概率
  • 观测概率矩阵 B，表示状态生成观测概率，$B[j][k]$ 表示 j 生成观测 k 的概率。

三大问题

评估问题：模型参数 - 观测序列

目标：

$$P(O|\lambda )$$

O 表示观测序列， $\lambda$ 表示模型参数。意为在参数模型的基础上，获得观测序列的概率。

前向算法：从初始状态开始，递推计算后续各个序列的概率。

$a_t(i)$ ：处于 t 时刻，状态 i ，且观测到前 t 个数据的概率

初始化，计算 t=1 的概率值：

$${\alpha }_1(i)=\pi [i]\cdot B[i][o_1]$$

递推，从 t=1 开始，向后计算每个时刻的概率值：

$${\alpha }_t(j)=\sum _i{\alpha }_{t-1}(i)\cdot A[i][j]\cdot B[j][o_t]$$

使用状态转移矩阵和观测矩阵，计算一个累加，获得当前状态的概率。

终止，一直计算到 t=T 的最终状态。

$$P(O|\lambda )=\sum _i{\alpha }_T(i)$$

与此类似的，还有后向算法，逆向计算后向概率 ${\beta }_t(i)$

解码问题：模型参数和观测序列 - 内部状态

目标：

$$Q\ast =\arg \underset{Q}{\max }P(Q|O,\lambda )$$

维特比算法：利用动态规划，求解最优路径

递推公式：

$${\delta }_t(j)=\underset{i}{\max }[{\delta }_{t-1}(i)\cdot A[i][j]]\cdot B[j][o_t]$$

解释：

• ${\delta }_t(i)$ ： t 时刻到达状态 i 的最大概率
• ${\psi }_t(i)$ ：记录路径
• 对当前状态，取上一个状态的最大值求解。
• 每一个状态的计算的 A B，转移矩阵和概率矩阵

学习问题：观测序列 - 模型参数

EM算法：利用两个期望直接更新参数

• E 步：计算期望统计量，状态转移期望 ${\xi }_t(i,j)$ ，状态占用期望 ${\gamma }_t(i)$
• M 步：利用期望更新参数：
  • ${\pi }_i^{\prime }={\gamma }_1(i)$
  • $A[i][j{]}^{\prime }=\frac{{\sum }_{t=1}^{T-1}{\xi }_t(i,j)}{{\sum }_{t=1}^{T-1}{\gamma }_t(i)}$
  • $B[j][k{]}^{\prime }=\frac{{\sum }_{t:o_t=k}{\gamma }_t(j)}{{\sum }_{t=1}^T{\gamma }_t(j)}$