《计算之魂》 - 10 确定与随机

确定性与随机性是计算机中的基本概念，随机性在加密领域和近似中都有应用，是非常有用的思维。

历史背景

19世纪查尔斯·巴贝奇发现差分机实现的是确定性计算
1930年代爱因斯坦与玻尔关于随机性的著名论战中，作者更认同玻尔”世界具有本质不确定性”的观点
现代大数据方法的核心：从海量随机数据中挖掘确定性规律

10.1 信息指纹：确定性与随机性的结合 P324

信息指纹原理

将确定性数据映射为随机数作为唯一标识
比较数据只需比较指纹，无需处理原始数据
思考：这与哈希计算的本质相同
关键限制：数据压缩不能小于其信息熵

例题10.1：信息重复概率计算

计算128位信息产生多少位后重复概率>50%：

第k个指纹重复概率公式：

P_{k} = \frac{N ( N - 1 ) \dots ( N - k + 1 )}{N ^{k}} = \frac{( N - 1 ) \dots ( N - k + 1 )}{N ^{k - 1}}

随机挑选 k 个数，令其不重复，这里使用的是二项式系数来表示选择数。

使用斯特林公式计算近似：

P_{k} \approx e x p (- \frac{k ( k - 1 )}{2 N})

解不等式 $P_{k} \leq 0.5$ 得：

k \geq \frac{1 + 1 + 8 N ln 2}{2}

思考误区：简单使用1/N计算会忽略累积概率的影响

思考题10.1：优惠券问题

本质是计算期望值的无穷级数问题
对于成功概率1/2的事件，期望次数为：

E = 1 \times \frac{1}{2} + 2 \times \frac{1}{2 ^{2}} + 3 \times \frac{1}{2 ^{3}} + \dots

详细解析见知乎文章

10.2 随机性与量子通信

加密安全基础

克劳德·香农证明：基于完美随机性的”一次性密码本”是理论上不可破解的加密方式

量子通信的BB84协议

物理基础：
- 光子偏振特性：45度偏振测量结果完全随机
- 定义两组编码基：垂直/水平和45/135度偏振
密钥协商过程：
- 发送方随机选择编码基发送光子
- 接收方随机选择测量基，产生25%错误率
- 通过公开比对筛选出正确测量结果作为密钥
抗中间人攻击：
- 中间人接受数据时，光子的偏振状态无法恢复，窃听导致误码率升至56%，就可以识别出中间人攻击。
- 通过霍夫丁不等式计算，仍然可能达到 75% 以上的正确率，概率低至 $1 0^{- 35}$

思考题10.2

均匀硬币连续20次正面朝上概率> $75%$ ?
20次中出现15次正面时，有多大把握认定硬币不均匀？

10.3 置信度：效果与成本的权衡 P333

置信度（Confidence level）表示当前方案在多大可能性下是管用的。

对结果的近似，不同的方法存在不同的置信度，对金店方法做改进达到不同的置信度效果，称为置信度下的优化

AlphaGo的近似策略

纵向简化：引入马尔可夫假说限制决策步长
横向简化：应用剪枝策略缩减博弈树宽度
效果：计算量降至原方法的百万分之一

维特比算法的近似优化

算法复杂： $O (K^{2} L)$ ，从左往右一列列计算最短路径问题。
- 相对而言，比 $O (K^{L})$ 的暴力搜索算法容易
- K：网络图的深度
- L：网络图的列数
剪枝策略之后的维特比算法称为聚光搜索

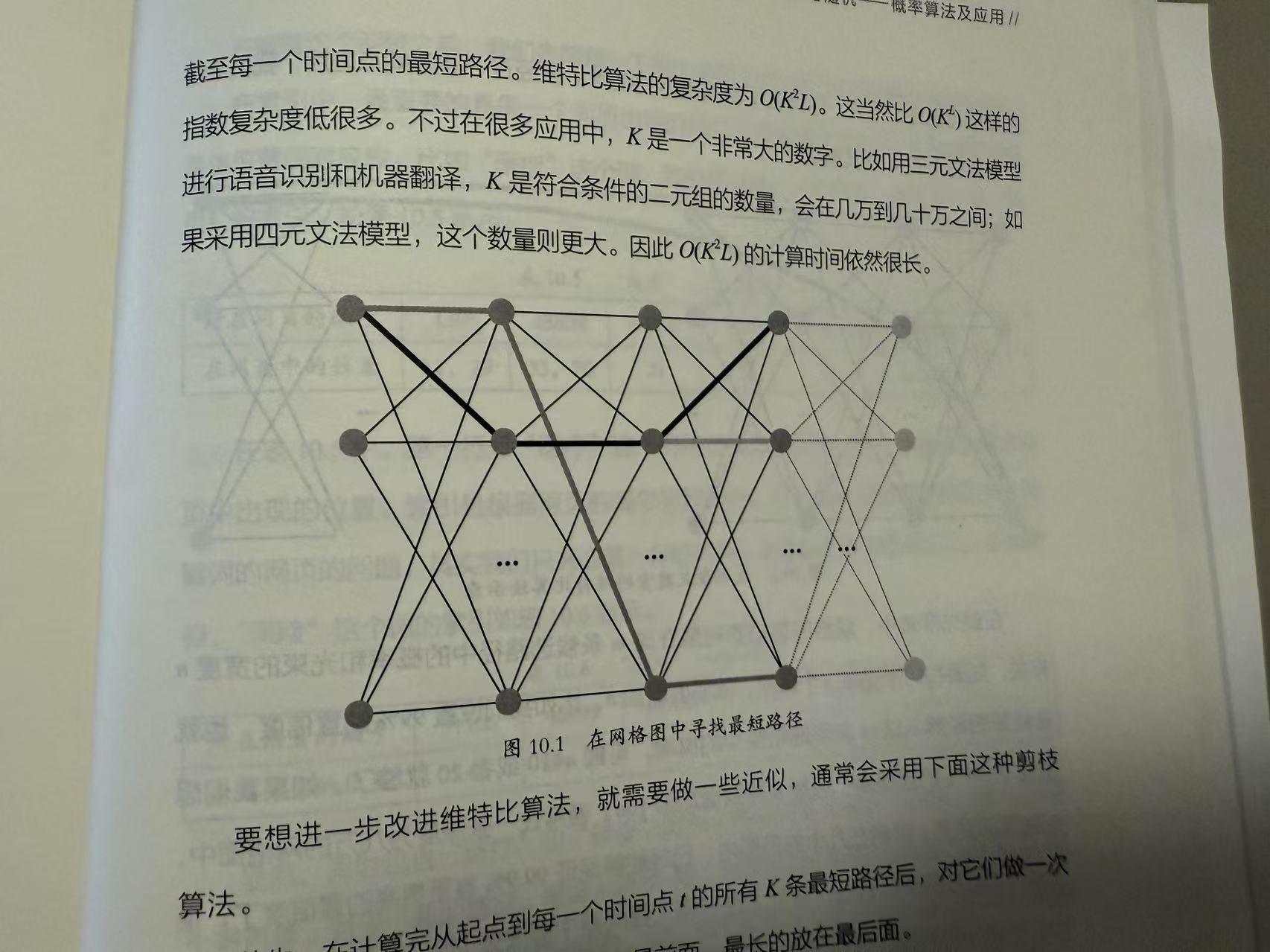
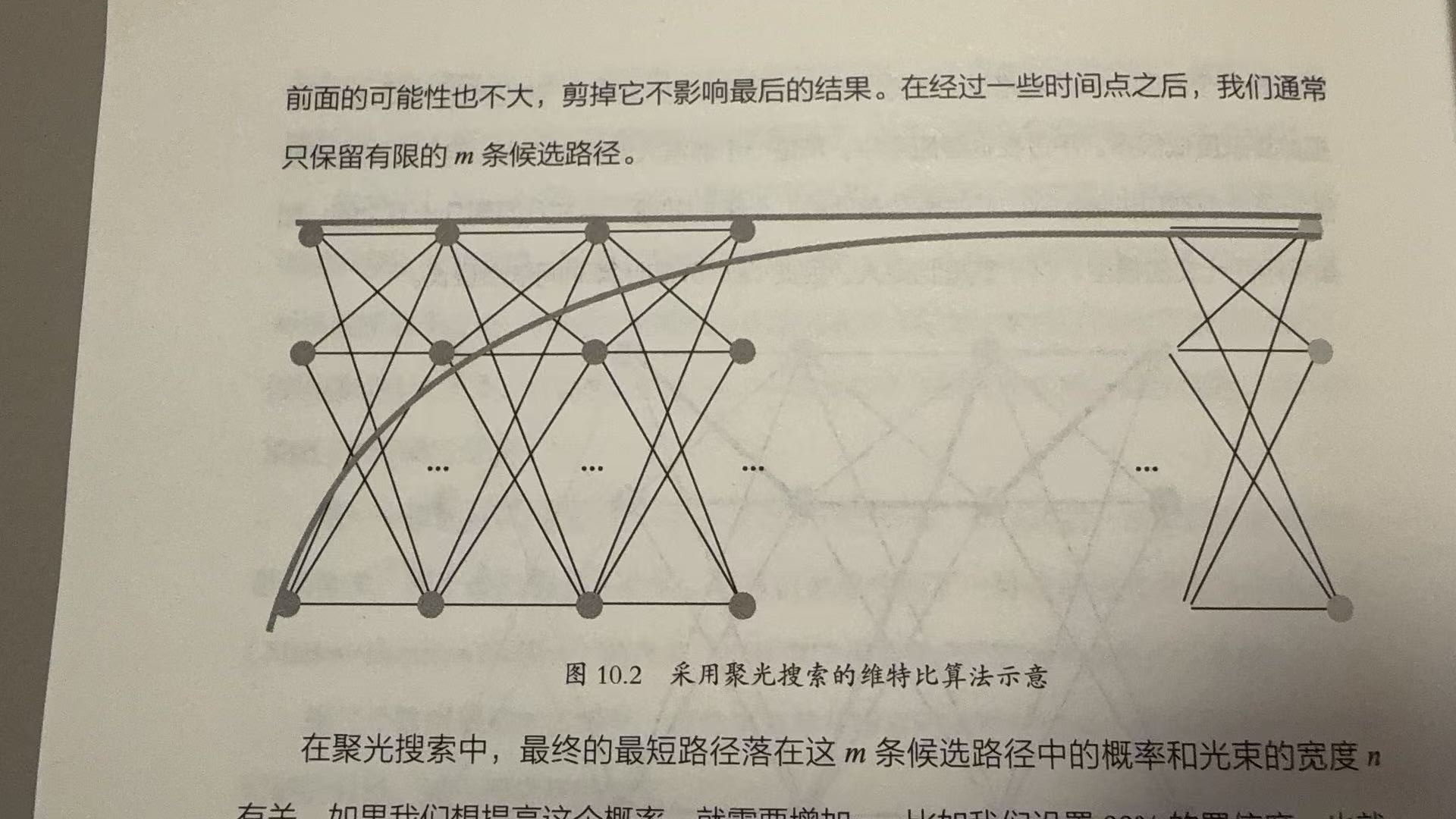
在每一个时间点 t 计算最短路径后，从高向低排序，保留top m路径，复杂度降为 $O (m K L)$
置信度与m值正相关

例题10.2：网页索引求交，同时找到两个包含不同词的网页，例如 X，Y

基本情况：X Y 的索引是用顺序编号保存。

基准方法：
- 归并排序法： $O (L (X) + L (Y))$
- 定量优化，将索引多的词汇做成哈希表，优化后得到： $O (min (L (X), L (Y)))$

左右附近搜索和索引：因为索引在词汇中存在分散性，使用哈希表方法优化：遍历索引较短的词，然后在另一个词的编号中预估网页编号可能出现的位置，然后在左右附近搜索。这样的效率虽然没有哈希表高，但是有着和哈希近似的计算复杂。

近似优化：
- 利用索引分布特性进行预估搜索
- Google实际应用：
  - 谷歌的近似结果：事实上在 Google 每次搜索中，给出的网页数量的结果也是一个估计值而非真实值
- 对搜索少结果的优化：对不到 10 个搜索结果的查询使用基准方法，而不是近似方法

思考题10.3：分布感知优化

如果知道是均匀分布，那么就可以估算随机数在数组中的位置，然后可以按照一定的方差在周围寻找目标值
如果知道是指数分布，那么也可以做类似的估算，不过与均匀分布不同，越靠前的值概率越高。

阿森知识库

探索