矩阵

线性代数中的基本概念，使用一组线性关系的二维数组。

空间的映射关系理解

范数对于数学的意义？1范数、2范数、无穷范数该怎么用？ - 知乎

矩阵可表示空间中的映射关系。而矩阵的“范数”，则是描述矩阵特征的向量。

ref: 图与矩阵

图与矩阵有等效关系，图中顶点用矩阵的行列表示，边及其权重为矩阵中的值。

ref:

《计算之魂》 - 3 编码思维

矩阵乘法 - 维基百科，自由的百科全书

公式表示为：

z_{i, j} = s = 1 \sum N x_{i, s} \cdot y_{s, j}

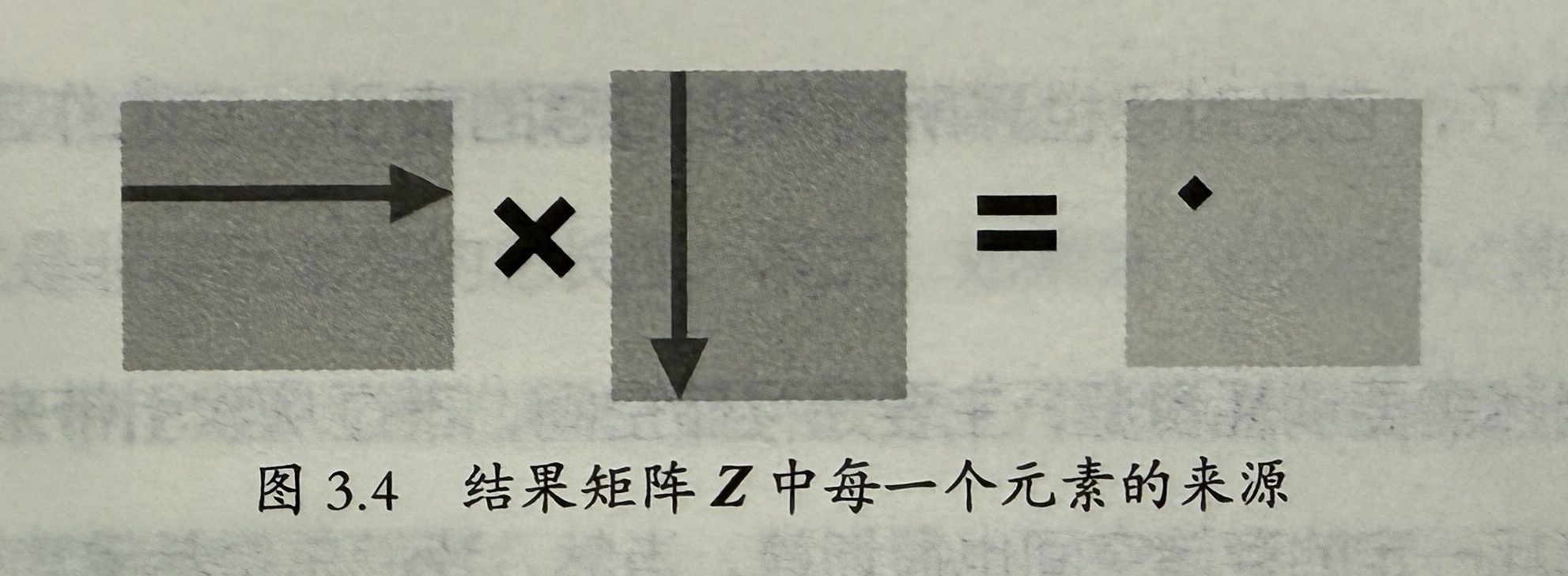
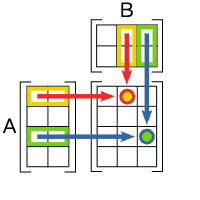
矩阵乘法即为横竖交错乘法，加求和方式。

ref: 理解矩阵乘法 - 阮一峰的网络日志

矩阵乘法等效于线性方程式的乘法。

${2 x + y = 3 4 x + 3 y = 7$ 等效于 $(2413) (y x) = (7 3)$

{a_{11} x_{1} + a_{12} x_{2} = y_{1} a_{21} x_{1} + a_{22} x_{2} = y_{2} (a_{11} a_{21} a_{12} a_{22}) (x _{2} x _{1}) = (y _{2} y _{1})

与

{b_{11} t_{1} + b_{12} t_{2} = x_{1} b_{21} t_{1} + b_{22} t_{2} = x_{2} (b_{11} b_{21} b_{12} b_{22}) (t _{2} t _{1}) = (x _{2} x _{1})

相乘，结果为：

{(a_{11} b_{11} + a_{12} b_{21}) t_{1} + (a_{11} b_{12} + a_{12} b_{22}) t_{2} = y_{1} (a_{21} b_{11} + a_{22} b_{21}) t_{1} + (a_{21} b_{12} + a_{22} b_{22}) t_{2} = y_{2} (a_{11} b_{11} + a_{12} b_{21} a_{21} b_{11} + a_{22} b_{21} a_{11} b_{12} + a_{12} b_{22} a_{21} b_{12} + a_{22} b_{22}) (t _{2} t _{1}) = (y _{2} y _{1})