《计算之魂》 - 3 编码思维

3.1 人与计算机编码习惯的区别

人与计算机编码的差异主要来自于目的不同：计算机以效率编码，讲究信息论的原理；人以方便编码，以方便辨识为目标。好的计算机工程师往往能站在计算机的角度审视自己的想法，而不是只站在人类的角度看问题。

许多设计不好的编码系统存在的问题往往是：没有设计好人与计算机编码之间的桥梁。例如：

高级编程语言是设计得比较好的桥梁
中国的邮政编码却是设计较差的桥梁

编码对应的是计算机中的位运算。

3.2 黄金分割问题

如何将一个金条切两刀，分成七份发工资？

一份1/7，一份 3/7，第一天支付 1 ，第二天支付 2，第三天支付 1+2，第四天 4，第五天 4+1，第六天 4+2，第七天 4+2+1

3.3 小鼠实验问题的感想

这个问题考察了编码思维和试验思维。在产品的AB测试中，往往会使用组合的方式来一次性测试很多产品特性，这样既节约时间又能保证测试的效果。

3.4 数据的表示，精度和范围

IEEE 754浮点数

使用32位或64位来编码浮点型数据。

两个玻璃球问题 - 粗调和精调问题

在1～100层之间使用两个玻璃球来试验玻璃球摔碎的层数

用编码思维解题：

两个玻璃球可以编码为个位和十位
解决粗调和精调的问题

粗调和精调思维

大的数字和大的数字一起处理
小的数字和小的数字一起处理
否则会出现计算溢出或精度被忽略
先粗调，再精调

计算机中很多地方需要用到这个思路，例如查找、训练和计算

大数字和小数字一起处理，要么计算移除，要么精度被忽略，粗调和精调，对应梯度爆炸和梯度消失问题。统称梯度问题。

3.5 非线性编码 P116

脉冲编码调制(PCM)

一般的编码方式。

差分编码

对关键帧做差量编码，可以用较小的数据量表示一串编码。

有规律的渐变是我们这个世界信息存在的普遍现象。

压缩技术

无损压缩和有损压缩是两种不同方式
根据香农第一定理，无损压缩的总长度不可能小于信息熵

3.6 哈夫曼编码

基本原理

较短的编码：分配给常见的信息
较长的编码：分配给不常出现的信息
可以有效节省信息传输带宽

编码要求

需要根据概率分布找到平均编码长度最短的方式
接近信息熵的极限
编码前要设置颗粒度，不同颗粒度的编码效率可能差别很大

计算步骤

将所有信息按照概率从小到大排序
概率最小的信息合并
重复步骤2，每次合并最小的两种信息，然后插回列
直到所有的信息合并在一起

有效性证明 P134

假设一种最短的编码，然后对编码的任意两个顺序置换，证明得到的编码长度大于当前的编码即可。

3.7 矩阵的有效表示

背景：矩阵一般计算包括加减乘除，其中需要关注的是矩阵乘法。

假设 A x B = C。那么乘法时就是 A 按“行”乘以 B 的“列”。在取数据时，A 按行取，B 按列取。于是有了以下的矩阵表示法。

按位置表示的乘法公式为：

z_{i, j} = s = 1 \sum N x_{i, s} \cdot y_{s, j}

稀疏矩阵

在计算机应用中，一般都是稀疏矩阵，使用索引的方式表示矩阵中的各个元素，可以减少矩阵占用空间。

矩阵的压缩表示方法

一个稀疏矩阵可以用 4 个表表示：

非零元素列号表：列和具体的值
每一行非零元素起始位置：行的指针
非零元素行号表：行和具体的值
每一列非零元素起始位置：列的指针

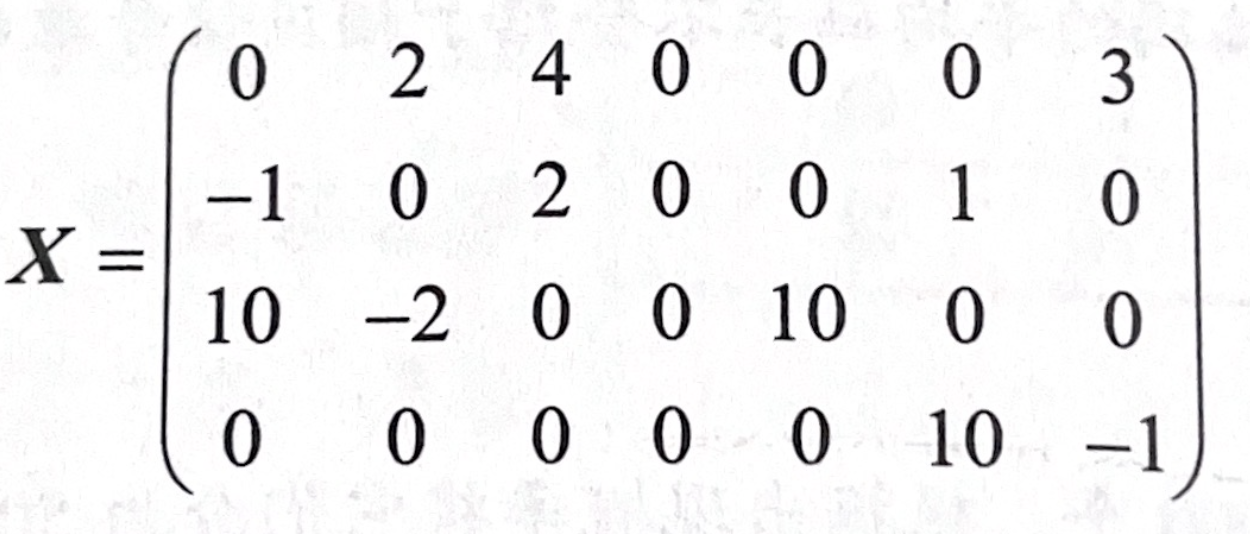
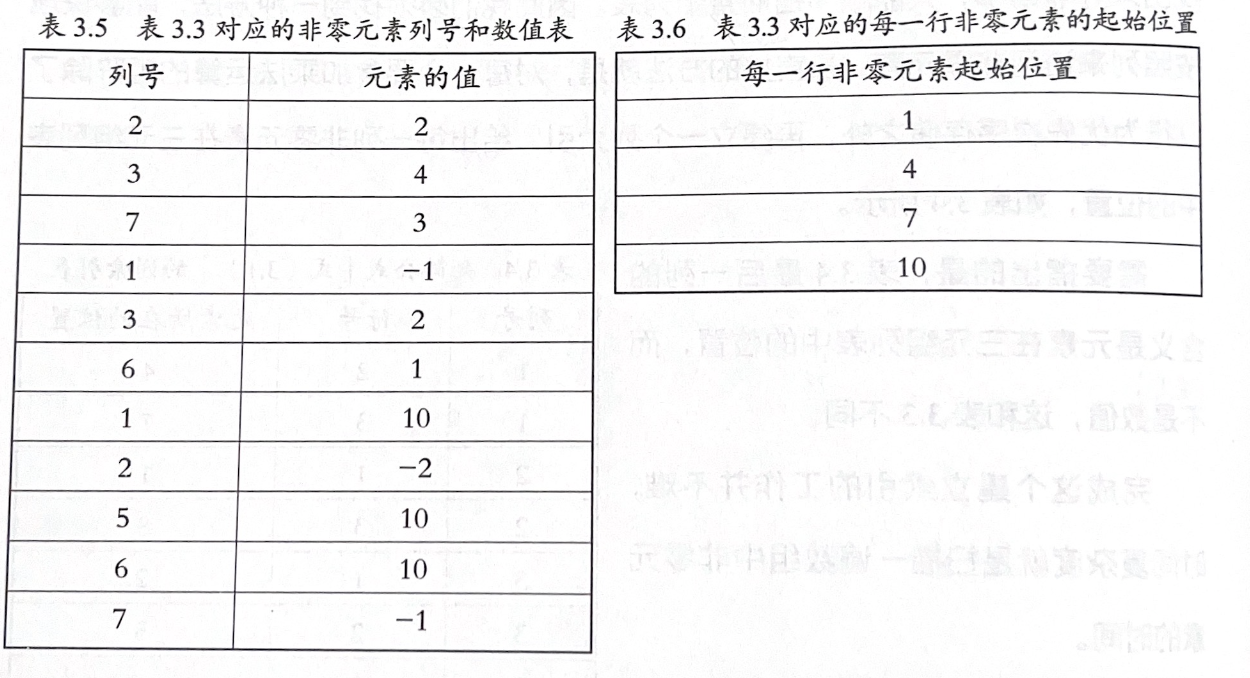
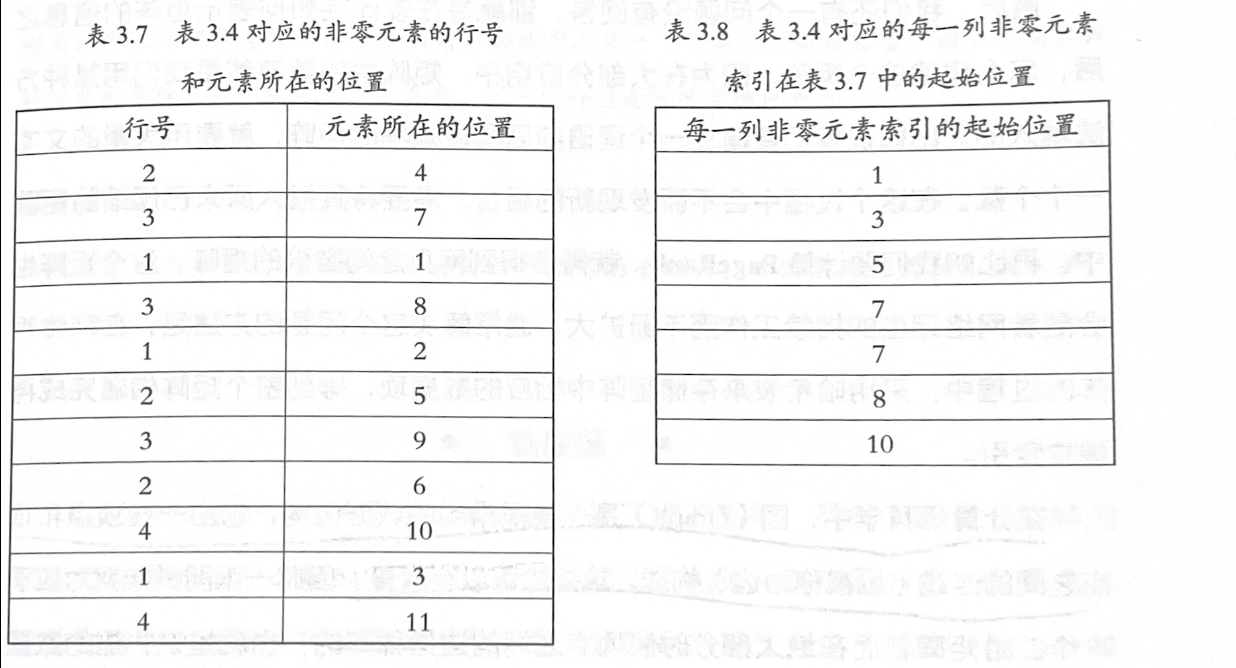
索引表中没有元素值，原因：

冗余性：多余的冗余数据不好修改，难以同步
矩阵过大的情况下，会造成占用空间过多。

理解：列索引表里面不存储行号可能也可以压缩，但为了计算效率，依然保留了行号。

图与矩阵

图与矩阵是等效的表示，连接可以表示为矩阵中的数值。

理解：在编码思维中，最关键的把握二分原则，因为计算机是二进制的，可以表示任何信息，永远要想办法挤掉多余的冗余信息。

阿森知识库

探索