卡特兰数

Catalan Number

卡特兰数表示一组递增数列，用于解决特定的排列匹配问题，有时候呈现为计数问题。

记忆点：

• 生成函数
• 二项式系数

ref:

• 《计算之魂》 - 4 分类与组合思维
• 卡特兰数 - OI Wiki

数列表示

( H_0 )	( H_1 )	( H_2 )	( H_3 )	( H_4 )	( H_5 )	( H_6 )	…
1	1	2	5	14	42	132	…

公式

解析解：

$$H_n=\frac{\left(\genfrac{}{}{0ex}{}{2n}{n}\right)}{n+1}(n\ge 2,n\in {\mathbf{N}}_{+})\text{\hspace{1em}(1)}$$

递推解和其他几个公式：

$$H_n=\{\begin{array}{ll}{\sum }_{i=1}^n{H}_{i-1}{H}_{n-i}& n\ge 2,n\in {\mathbf{N}}_{+}\\ 1& n=0,1\end{array}\text{\hspace{1em}(2)}$$

• 语义：第 n 个卡特兰数是之前所有卡特兰数的交错相乘求和。类似于卷积形式。
• 理解：此公式揭示了可解问题的基本形式“交错组合求和”。

$$H_n=\frac{H_{n-1}(4n-2)}{n+1}\text{\hspace{1em}(3)}$$

• 语义：递推式

$$H_n=\left(\genfrac{}{}{0ex}{}{2n}{n}\right)-\left(\genfrac{}{}{0ex}{}{2n}{n-1}\right)\text{\hspace{1em}(4)}$$

• 理解：4 可以推导到 1 式，将二项式展开即可。

相关问题

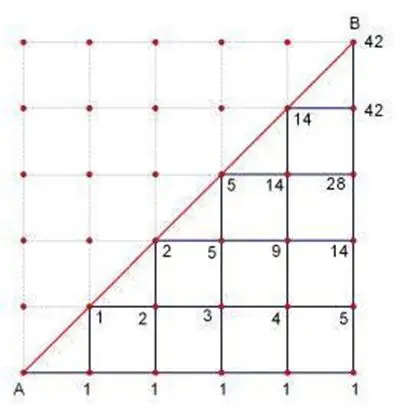
对角线图步行问题：

ref: 卡特兰数_百度百科

有一个大小为 $n\times n$ 方格图，左下角为 (0,0) 右上角为 (n,n)，从左下角开始每次都只能向右或者向上走一单位，不走到对角线 $y=x$ 上方（但可以触碰）的情况下到达右上角有多少可能的路径？