1.1 计算机算法的历史
计算机算法的历史可以追溯到1944年,冯·诺依曼设计了第一台真正意义上的通用计算机EDVAC,这也是冯诺依曼体系结构的首次实现。这一突破为现代计算机科学奠定了基础。
在算法研究领域,高德纳的贡献:
- 大O表示法:算法分析方法
- 经典著作《TAOCP》(《计算机程序设计艺术》)
1.2 大数和数量级的概念
高德纳提出的算法分析方法包含三个核心观点 P32:
- 大数定律:比较算法效率时,只需关注数据量趋近无穷大时的情况
- 随数据量变化的因素更加重要:固定因素和随数据量变化的因素,后者才是关键
- 数据量增大后的量级差距:即使复杂度差异很小,在大数据量时也会导致显著性能差距
大O表示法的核心原则是:当分析算法复杂度时,只考虑N趋近无穷大时与N相关的部分,常数项可以忽略。这个概念帮助我们聚焦算法最本质的效率特征。
葛立恒数:这个超越常规表示法极限的超级大数,展现了数学中数量级的惊人可能性。
1.3 寻找最优算法
最大子序和问题:给定实数序列,找到总和最大的区间。在股票问题上,就是“寻找一只股票的最长有效增长期”。
算法优化过程:
-
三重循环的暴力解法,复杂度
-
滑动窗口优化,两重循环, 给定起点,一步一步往后滑动到结束点。期间不断加入新的数据。
-
分治算法, 递归将序列一分为二,分成 1~K/2 和 K/2+1 ~ K 的两个子序列,找到,比较子序列邻接序列,最终找到最大子序列。
拼接有两种情况:
- 两个最大子序之间完美拼接,那么直接取从第一个子序的起始位置到第二个子序的结束位置。
- 如果两个最大子序没有邻接,[p1, q1],[p2, q2],那就情况三选一: [p1, q1], [p2, q2], [p1, q2]
拼接完成之后递归即可。
- 正反扫描, - P38 令 S(p,q) 为起始为 p,结束为 q 的序列和。
先正向扫描求和,求序列 S(1,p),找到最大数 Maxf,然后反向扫描求和,求 S(p,n),找到最大数 Maxb,两数之间为最大子序列。 复杂度实际上是 2K,用大O表示成为K。
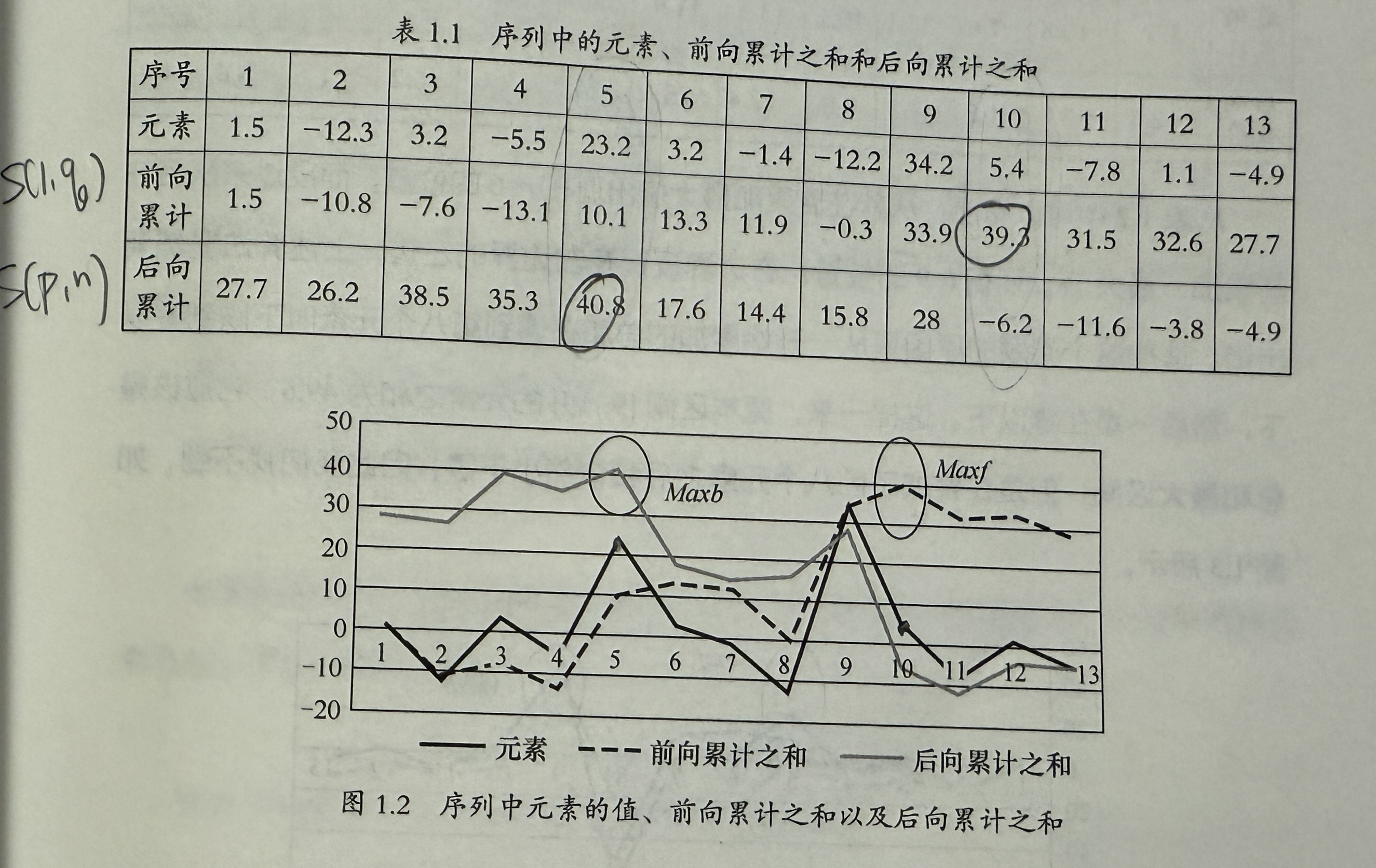
特殊情况,在 q 某个地方小于零,然后一直小于零。前后项给出的结果无法拼接。
解决方法是将区间在 q 处中断,另起区间进行前后向计算:先固定正的左边界,p,一旦 S(p,q) < 0 则算法在 q 中断,获得区间 [l1, r1],然后继续计算,获得区间 [l2, r2]。
比较两个区间的最大值后获得结果。
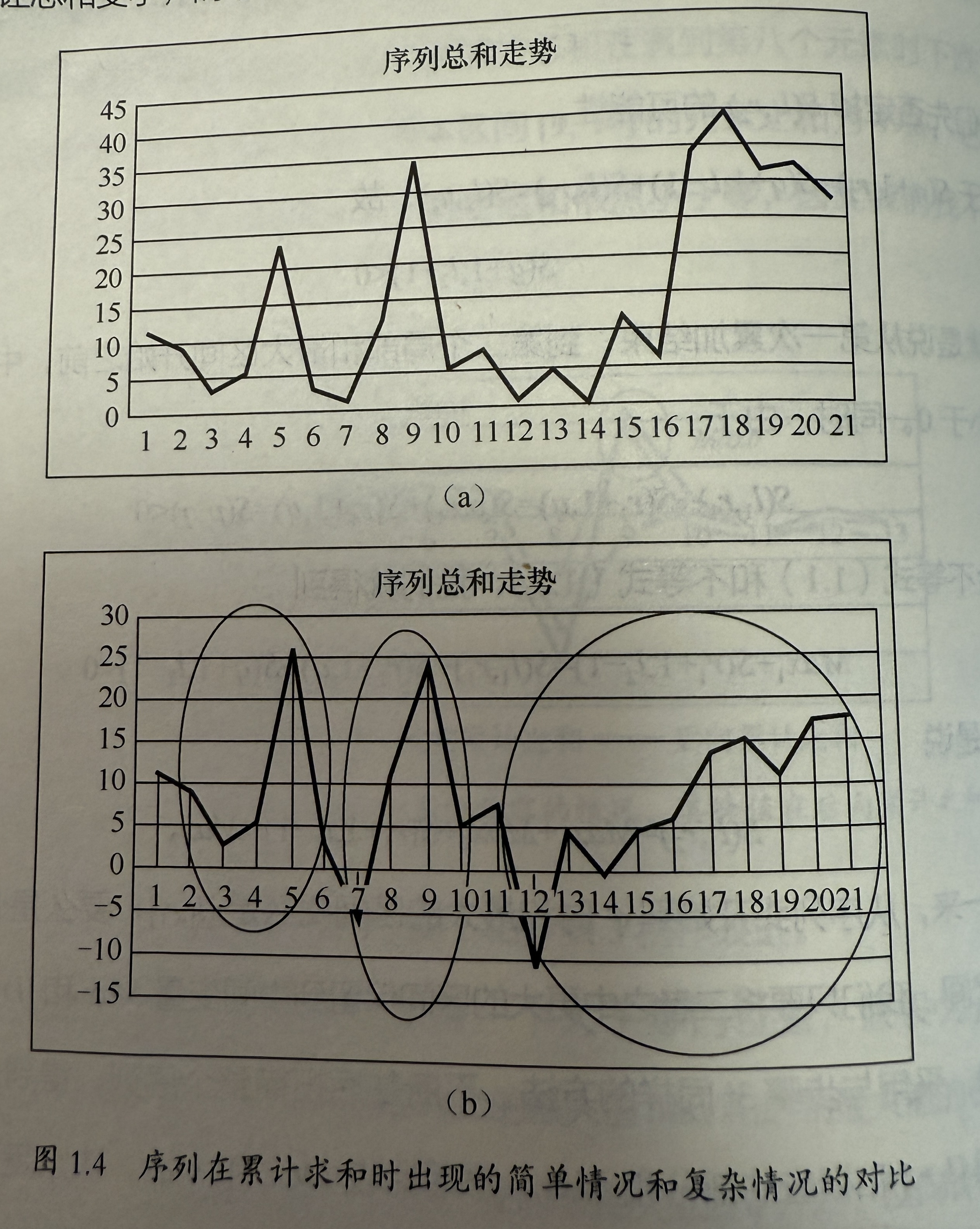
- 示例中区间被拆成了三个部分。
总结:算法优化直觉关键:
- 起始边界:确定必要的边界扫描
- 无用功:识别并消除无效操作
- 逆向思维:尝试逆向思维寻找突破口
1.4 排序算法演进
1.4.1 基础排序算法
选择排序和插入排序虽然直观,但都存在 的时间复杂度瓶颈。选择排序的无效比较和插入排序的数组搬移操作都导致了效率低下。
1.4.2 高效排序算法
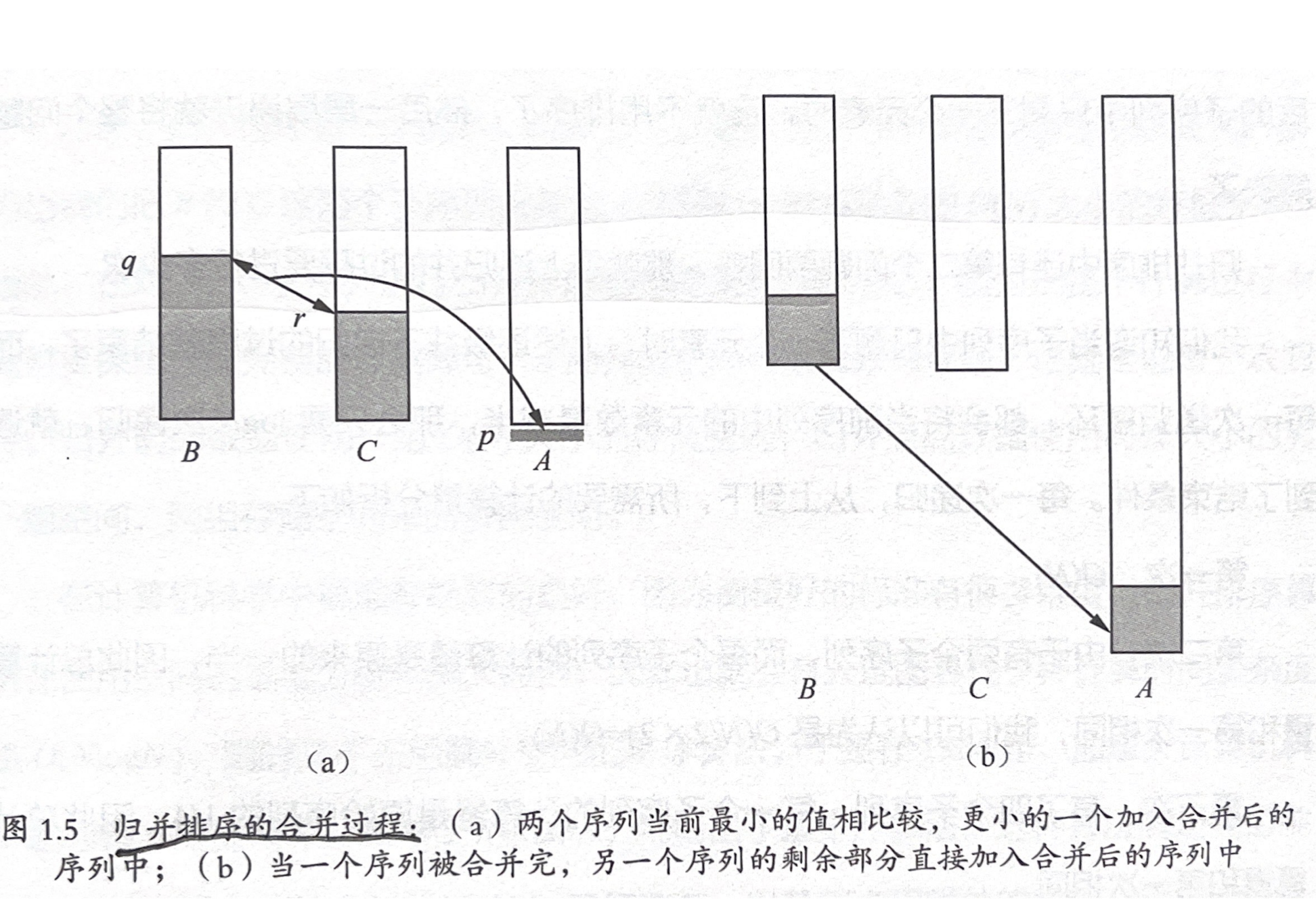
- 归并排序(冯·诺依曼提出): 假设序列 a 和 b 都是已排序序列,每一次归并,将子序列头部的元素一个一个比较,然后放入新序列。属于分治排序策略,需要额外存储空间。
| 算法 | 平均时间复杂度 | 最坏时间复杂度 | 额外空间 | 稳定性 |
|---|---|---|---|---|
| 归并排序 | O(NlogN) | O(NlogN) | O(N) | 稳定 |
| 堆排序 | O(NlogN) | O(NlogN) | O(1) | 不稳定 |
| 快速排序 | O(NlogN) | O(N²) | O(logN) | 不稳定 |
1.4.3 现代实践
蒂姆排序(结合插入和归并排序)因其优异表现成为Python的默认排序算法。它通过识别数据中的有序区块来提升效率。将每一个递增和递减块堪称整体进行归并排序的算法
1.4.4 排序复杂度下限
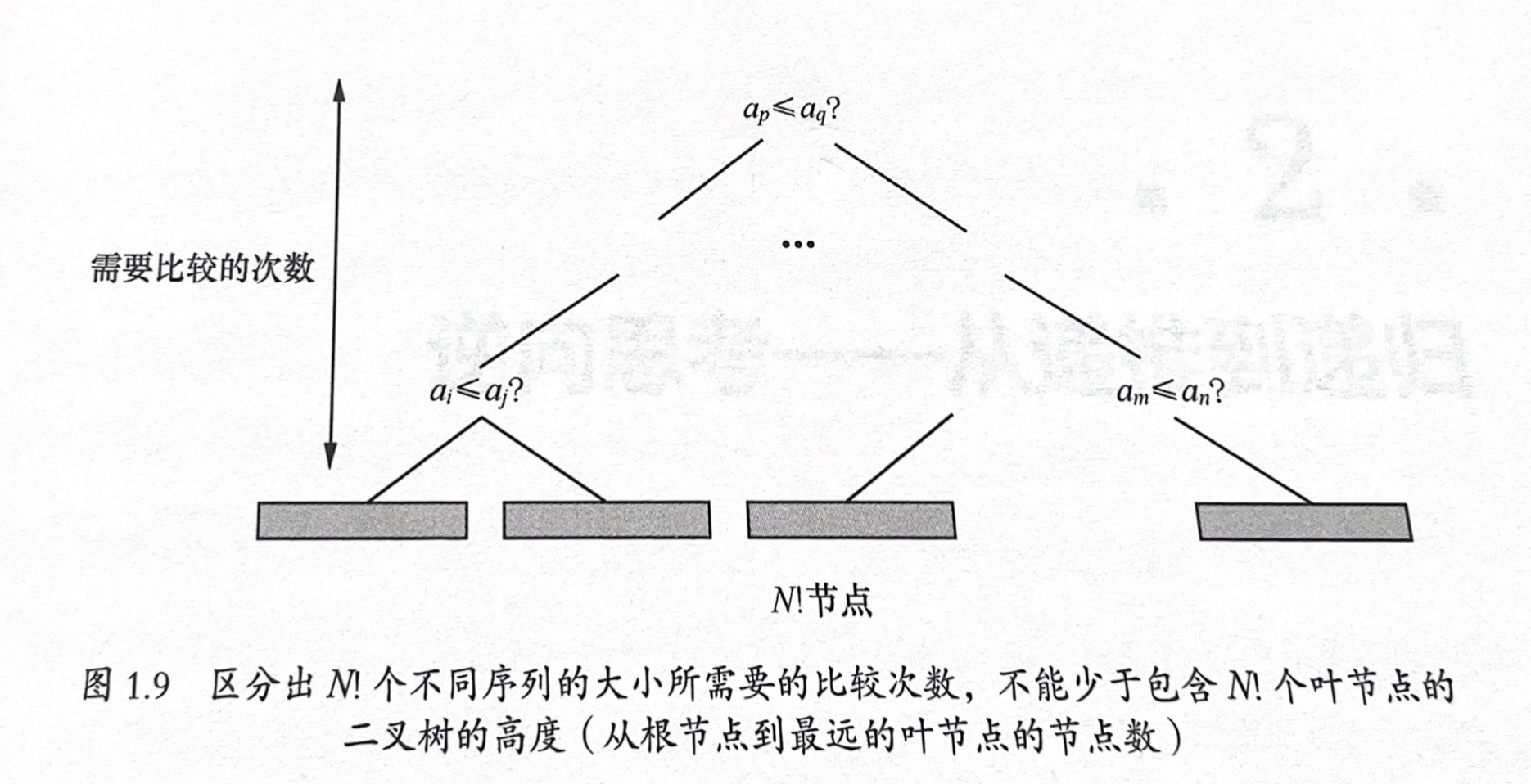
通过斯特林公式可以证明,基于比较的排序算法复杂度下限为O(NlogN)。这一理论界限帮助我们评估算法的优化空间。
思考题 1.4 赛跑问题
关于赛跑问题的深入讨论可以参考: 计算之魂思考题1.4——赛跑问题和区间排序