PCA

PCA = Principle Component Analysis

主成分分析

算法的目的是将高维的数据投影到低维的平面上。因为高维数据往往难以处理，而低维数据处理起来更加方便。

直觉

PCA 就是在一个数据集代表的线性空间中几个新的“方向”，这些方向能够代表数据最大的变化趋势。

关键词为“变化”和“映射”：

• 变化：在统计学中，协方差是不同变量之间线性相关性的量化表示，所以在计算 PCA 时要先计算协方差。
• 映射：而 PCA 计算过程中的矩阵乘法则对应了“映射”，因为我们知道矩阵的乘法往往是将一个矩阵中数据“投影”到了另一个平面的变换。

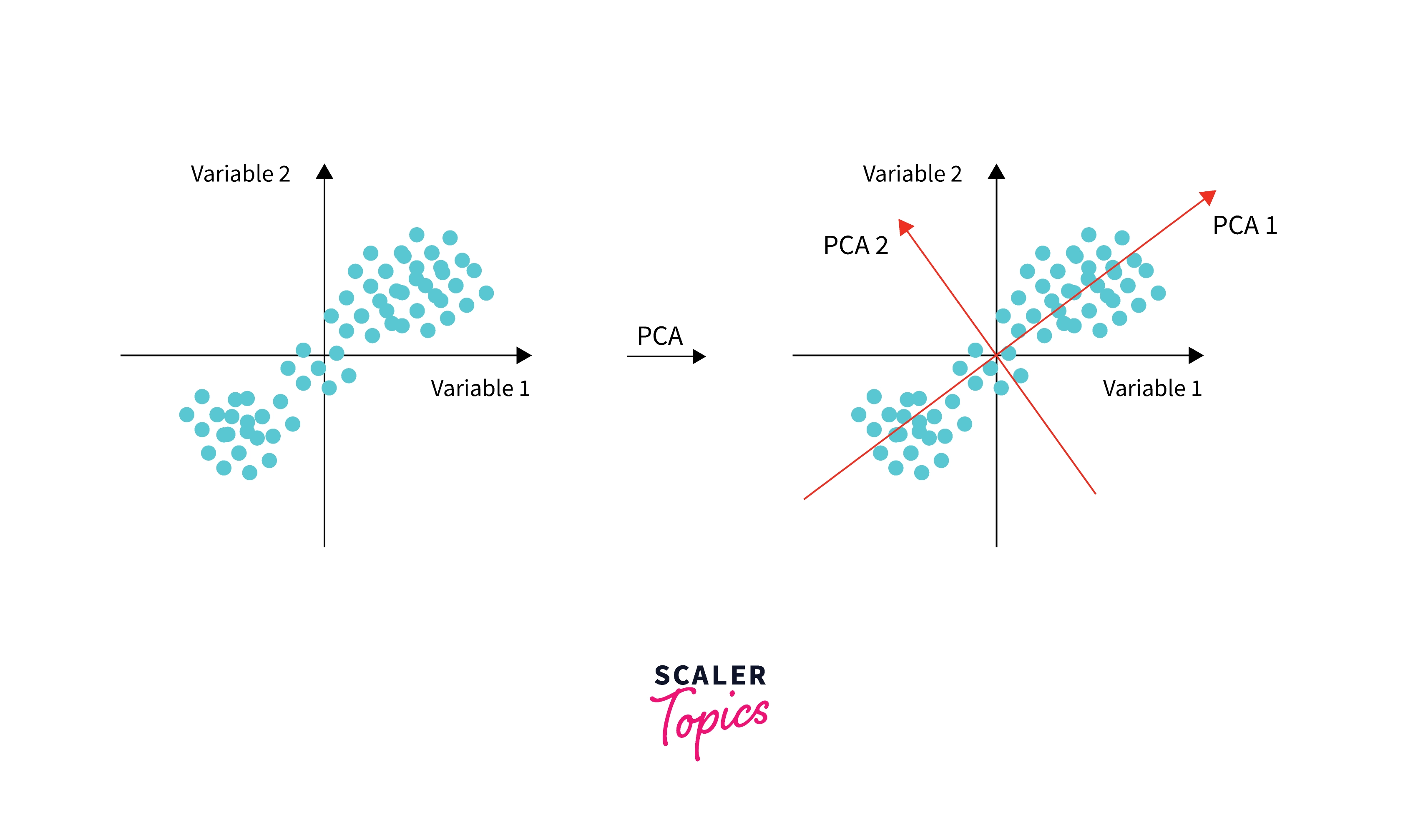
图中的红线就是特征向量的方向，PCA 通过特征分解的方式获得了“最能够代表数据变化”的两个方向。而一旦选中了其中一个方向而放弃另一个方向，就达成了“降维”的效果（二维变成了一维）。

步骤

首先，因为 PCA 本身也是一种算法，输入为待处理的数据矩阵，输出为降维后的数据矩阵。X 为一个数据集，$X_j$ 表示每个变量的数据集合。

观测	X1	X2
1	2	3
2	3	5
3	5	6
4	1	2

然后将其用五步处理：

第一步，预处理，保证每个维度上的数据均值为0，方差为1。因为 PCA 变换本身对数据的规模比较敏感，所以在处理前需要归一化。

$$X_j^{\prime }=\frac{X_j-{\mu }_j}{{\sigma }_j}$$

Xj 表示数据行的每个变量，式中将原值减去均值然后除以标准差来归一化。

第二步，计算协方差矩阵。协方差即为多个参数之间的方差。协方差矩阵描述了不同维度数据之间的关联关系。

$$\Sigma =\frac{1}{n-1}{X}^{\prime }{X}^T$$

X’ 是标准化后的数据矩阵转置。

第三步，对协方差矩阵做特征分解得到特征值和特征向量。

$$\Sigma v=\lambda v$$

v 为特征向量，$\lambda$ 为特征值。

第四步，选择主成分，例如前 k 个最大的特征值对应的特征向量。

第五步，利用特征向量转换原始的数据矩阵。

$$Y=X^{\prime }{V}_k$$

Vk 是由多个特征向量组成得到的矩阵。

特征

• 基于线性假设：PCA 的变换本身是线性的，更适合线性变换的数据计算。
• 无参数：直接就可以变换，无需更多参数，如果说非得要有的话，那就是那个 k。
• 正交性：PCA 得到的主成分是互相正交的，互相之间没有关联关系。