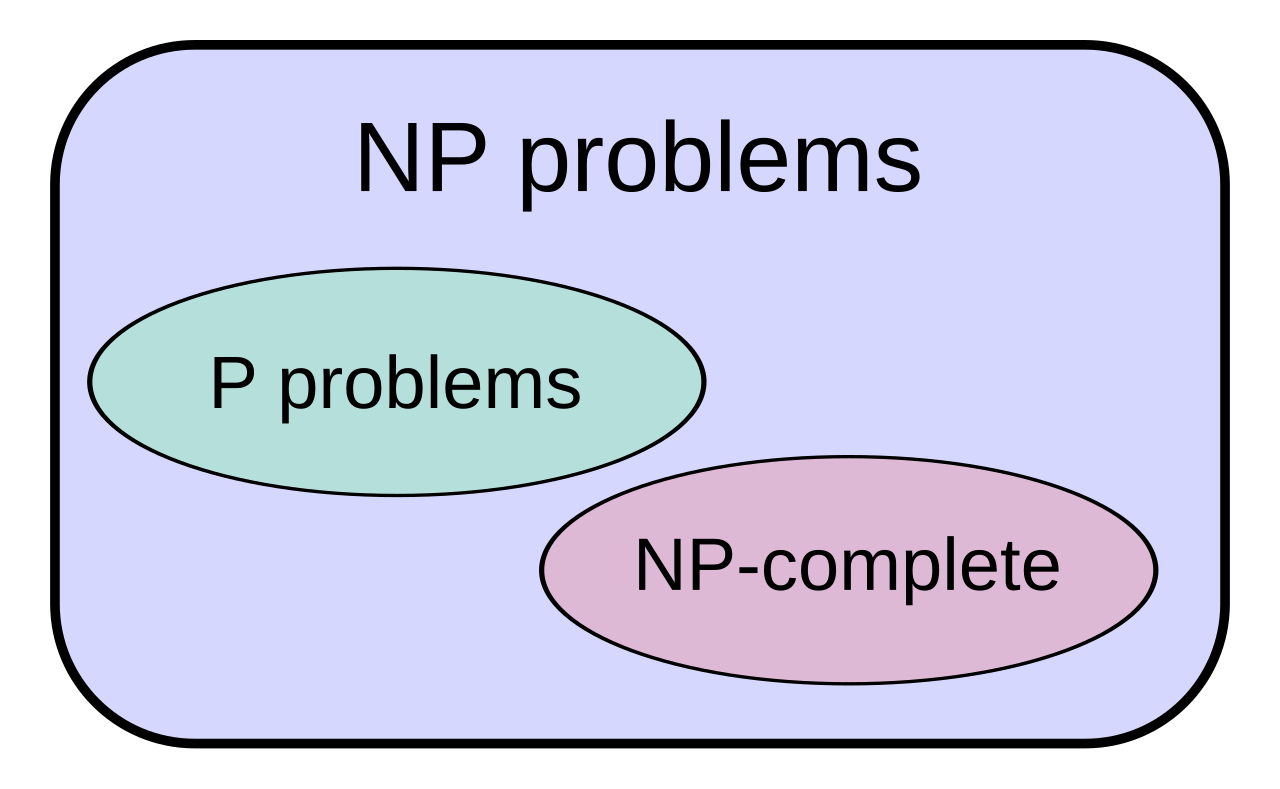
一个用集合论表示的,对于计算复杂度的子问题。用于明确可计算问题的复杂度极限。
概述
- P (Polynomial Time) 问题:在“确定性图灵机”上,所需要的计算时间不超过一个确定的多项式
- NP (Nondeterministic Polynomial Time) 问题:在“非确定性图灵机”上,所需要的计算时间不超过一个确定的多项式
P 和 NP 讨论的是判定问题,研究一个问题是否是可被判定为有解的。
理解
一般认为,一个问题可在图灵机上以多项式代价解决,那么这个问题就应该是“高效可解”的问题。
P 问题就是高效可解的问题。而 NP 则不一定。
由此引出 NP-完全问题。
NP-完全:如果有一个解,可被高效验证,但是如要搜索一个最优解,则无法高效解决。所以,NP-完全就是“复杂问题”的代表。
典型的 P 的例子是:排序问题;
典型 NP 的例子:旅行商问题
相互关系
在确定性图灵机上高效可解的问题,一定在确定性图灵机上高效可解,所以 P ⊆ NP。
但是 NP-完全则非常复杂,不属于 P。所以 P、NP、NP-完全的关系可以总结为: