《计算之魂》 - 6 分治思维

分治算法的三个理解层次

1. 基础应用：能够解决基本算法问题
2. 灵活运用：解决复杂现实问题
3. 创新突破：解决看似无解的问题

核心步骤：

1. Divide：将复杂问题分解为子问题
2. Conquer：递归解决每个子问题
3. Combine：合并子问题的解

分治算法的核心是分割与合并，分割可以使用递归

6.1 归并排序的分治思维

• 归并排序：将两个已经排好序的子序列通过移动指针的方式放到新的序列中。也就是”搬家排序“。
• 降低计算代价：分治思想将$O(N^2)$复杂度降低到$O(NlogN)$

伪代码

Merge-Sort(A, begin, end) {
    if (begin < end) {
        mid = lower_bound( (begin + end) ) / 2;
        Merge-Sort(A, begin, mid);
        Merge-Sort(A, mid+1, end);
        Merge(A, begin, mid, end);
    }
}

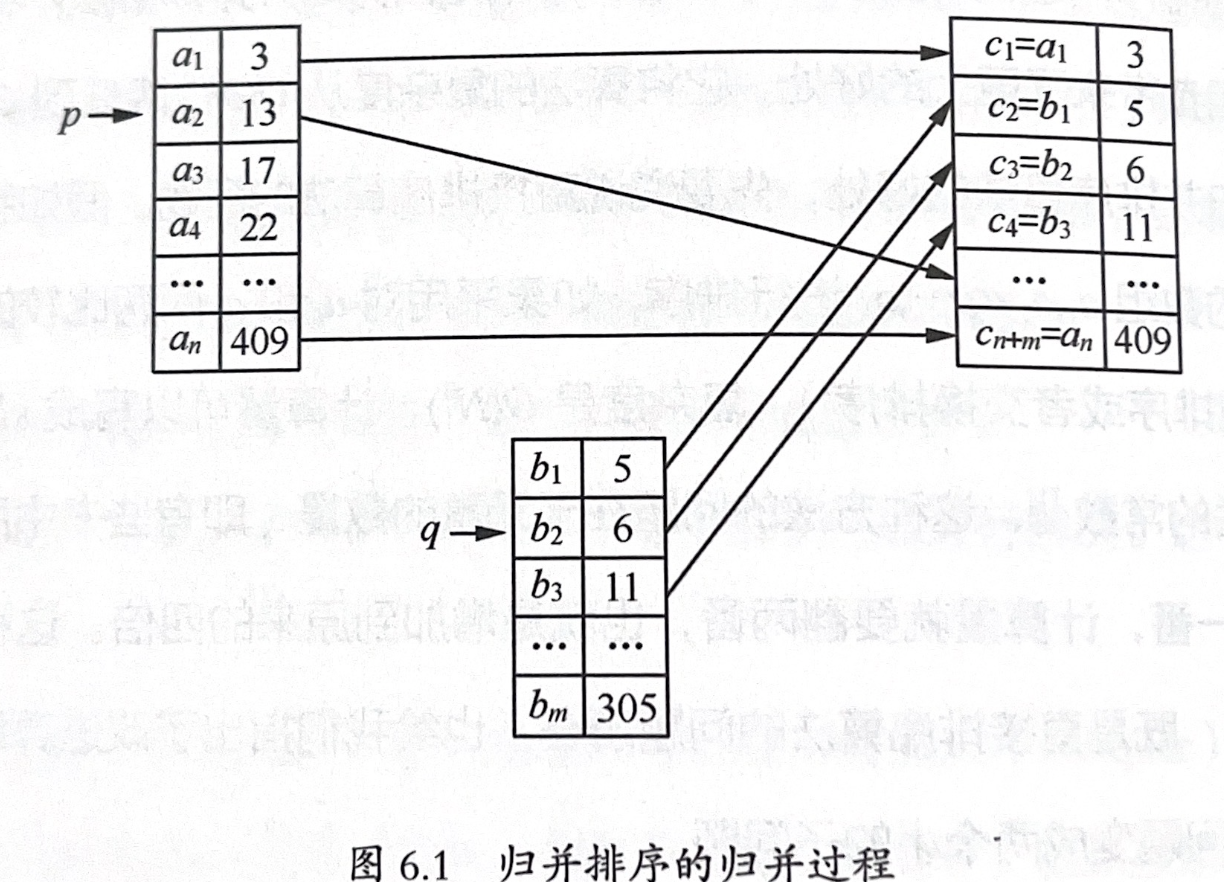
时间复杂度分析

归并排序的计算量表示为： $F(N)=2F(N/2)+kN$ 最终推导得到： $F(N)=2^{logN}\cdot F(1)+kNlogN=N+kNlogN=O(NlogN)$

思考题1.4：25人赛跑问题

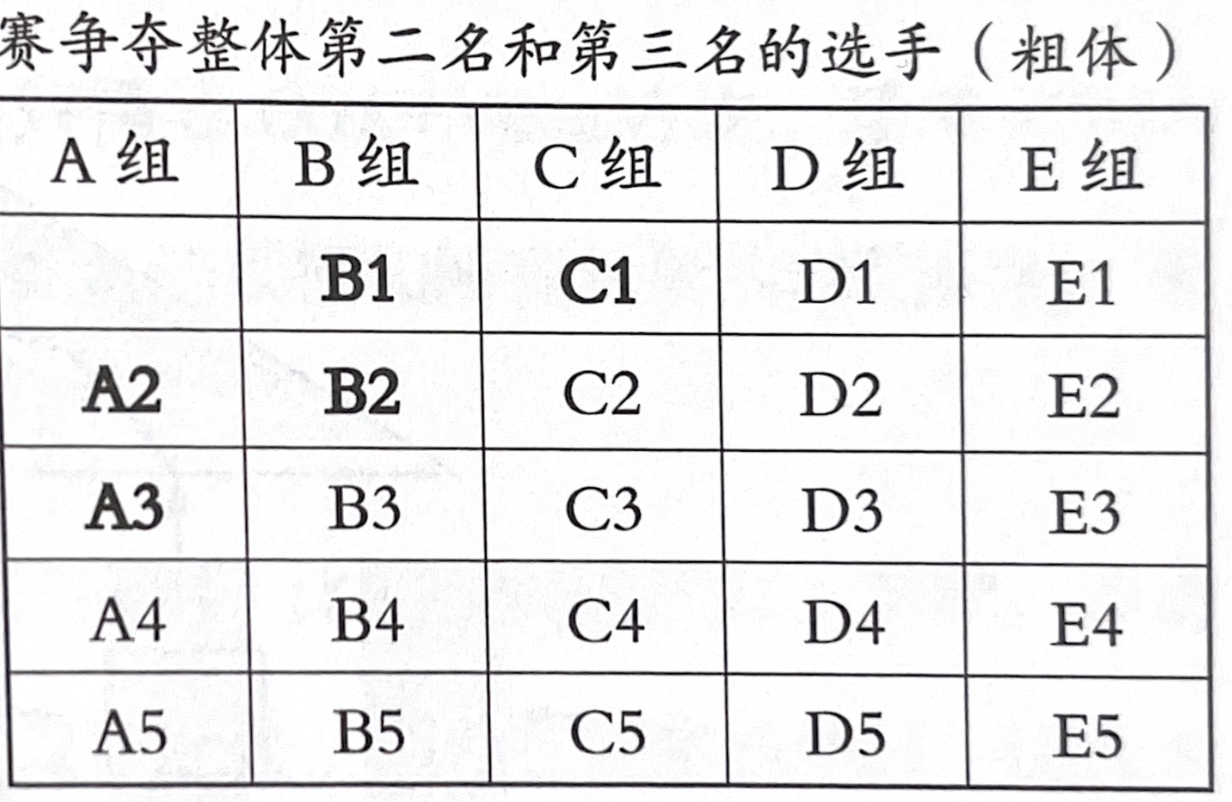
• 使用归并排序思维解决
• 关键点：避免重复计算，仅筛选可能成为第二、三名的选手
• 解决方案：先分组比赛选出每组前3名，再让这些选手比赛确定最终名次

例题 6.2 N 个排好序的序列中选出 K 个最大元素

堆排序：每次计算从排好的序列中选出最大值放在堆中，并执行堆重建，然后取出堆的根节点。一直执行下去直到排序完成。

计算复杂度为 $O((K+N)logN)$，挑选 K 个元素需要 $O(KlogN)$ 复杂度，建立一个 N 个元素的堆需要 $O(NlogN)$ 复杂度。

6.2 分割算法：快速排序和中值问题

例题 6.3：找出最大的K个元素

建立一个 K+1 小顶堆，然后每一步都把最小值拿掉，做一个 reheap 算法，然后每一次都把序列中下一个未处理的元素放进来，拿掉顶部最小值。直到所有元素都处理一遍，最后小顶堆里面剩下的元素就是最大的 K 个元素。

• 堆排序解决方案：复杂度$O((K+N)logN)$
• 更优方案：使用分割算法，复杂度$O(N)$

例题 6.4：在巨大的数组中找到中值，中位数问题。使用分割查找求解

每一次随机在数组中找一个数，再将小于这个数的值放在左边，大于这个数的值放在右边，看那边的数字更多，说明中值肯定在多的那一边，然后重复上述的计算。

假设每次都能剔除 1/3 的数字，那就总共计算量为3N，相当于整体扫描三次。考虑 几何级数 的计算法：

$$N+Nr+N{r}^2+...=\frac{N}{1-r}$$

分割查找伪代码

PartitionByRatio(A, start, end, target_position) {
    if (start < end ) {
        left_subarray_end = Partition(A, start, end);
        if (left_subarray_end == target_position) 
            return;
        if (left_subarray_end < target_position) {
            PratitionByRatio(A, start, left_subarray_end, target_position);
        } else {
            PartitionByRatio(A, start, left_subarray_end, target_position);
        }
    }
}

图示

分割查找的高效性

• 分割算法只需要寻找中值而不需要排序，省去 $O(logN)$ 的计算量
• 线性复杂度的算法比 NlogN 复杂度算法更高效，大数量级的计算下更是
• 利用分割算法求解 6.3，计算复杂度可以更低。N 选 K 只要按照 K:(N-K) 来取值即可

快速排序的分治算法

分割查找是快速排序的核心。从线性复杂度找到中值。

一句话总结：每次要挑选在序列中挑选一个枢值，然后对当前数组做一次分割，小的放左边大的放右边。然后每一次再对左右两边的子序列做相同的处理。最后将所有的序列合并，得到已排序的序列。

和归并排序的异同

• 快速排序在每次递归的时候在找枢值，而归并排序只是单纯的将序列划分成两个序列分开排序
• 快速排序和合并时不需要计算，但是归并排序需要额外计算
• 快速排序好像按照成绩来分班，归并排序好像随机分班。所以快速排序的效率会更高。

一个例子：

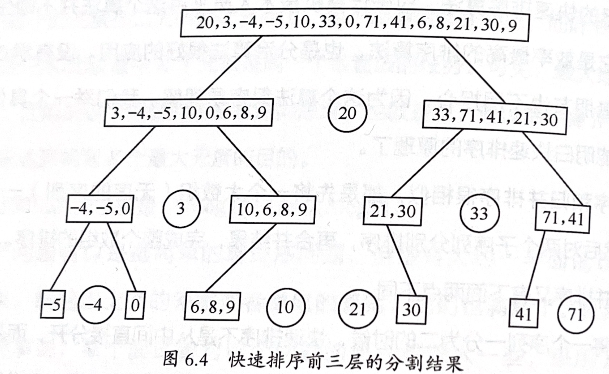
• 该例子中使用数组中的第一个值为”枢值“。

快速排序的伪代码

QuickSort(A, start, end) {
	if (start < end) {
    	left_subarray_end = Partition(A, start, end);
        QuickSort(A, start, left_subarray_end);  // 左子序列
        QuickSort(A, left_subarray_end + 1, end);  // 右子序列    
    }
}

Partition(A, start, end) {
	// 选择枢值
    pivot = A[start];
    left_position = start - 1;
    right_position = end + 1;
    while(TRUE) {
    	// 找序列左边第一个大于枢值的元素
    	repeat right_position = right_position - 1;
        until A[right_position] <= pivot;
        // 找序列右边往左找第一个小于枢值的元素
        repeat left_position = left_position + 1;
        until A[left_position] >= pivot;
        if(left_position < right_position) { // 序列没有比较完，则交换
        	A[left_position] 与 A[right_position] 交换;
        } else {
        	return right_position; // 如果序列比较完了，返回枢值的位置
        }
    }
}

计算复杂度的计算过程：

• 假设每一次分割，都将序列分为了 r:(1-r) 比例的两个序列
• 每一层的递归算法计算量大约为 N 次，每深入一层，计算量 - 1，但是可以大致认为计算总量为 NL，L 为层数
• 那么这样一来，就要进行$min\{lo{g}_{1/r}N,N-1\}$ 层的递归，就能保证分割到只有一个元素存在。
• 如果 r=2/3 那么大约为 1.7logN。但是当一个数列是已经排序好的情况，分割最没有效率，那么就是 $N^2$ 的复杂度
• 由此可见，快速排序算法的复杂度取决于枢值的选取

6.4a 中值问题的分布式版本

对于1000台服务器存储的数组：

只需要定义一个枢值，将枢值传输给不同的计算机，然后做分割计算。收集每个计算机大于枢值的数量 m 和小于枢值的数量 n，比较 m 和 n 选择新的枢值即可，最终找到中值的位置。

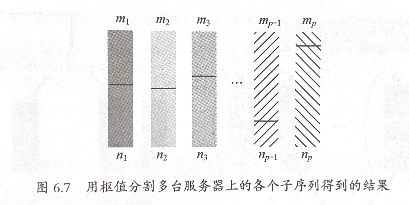
• 依然是线性复杂度
• 分布式中值问题和归并排序的问题：前者在大任务上循环，归并多次。后者在小任务上循环并归并一次。

TODO 继续工作

快速排序分析

快速排序是典型的分治算法：

1. 选择枢值并分割数组
2. 递归处理左右子数组
3. 无需合并步骤

复杂度分析

• 最佳情况($r=1/2$)：$O(NlogN)$
• 最差情况(已排序)：$O(N^2)$
• 实际效率取决于枢值选择

6.3 并行计算应用

并行矩阵乘法

两种主要架构：

1. 列表架构：
   • 按行或列分割矩阵
   • 通过共享部分矩阵减少通信
2. 矩阵架构：
   • 使用$N\times N$台服务器
   • 每台处理$1/N^2$的计算量

这些方法本质上是MapReduce的大规模应用

思考题6.3：网络传输限制

当传输速度是计算速度的1/10时：

• 10台服务器：速度提升约5倍
• 100台服务器：速度提升约9倍
• 1000台服务器：速度提升接近10倍

6.4 机器学习和深度学习

挑战

1. 参数矩阵与训练数据强相关
2. 参数间关联度高，难以拆分
3. 模型规模超过单机存储能力

谷歌大脑解决方案

1. 将神经网络分割为多个模块
2. 近似模拟模块间耦合性
3. 利用神经网络的对称性和容错性

思考题6.4：大矩阵求逆

可能的解决方案：

1. 分块矩阵法
2. 迭代法(如Jacobi迭代)
3. 并行计算结合分治策略

现代计算机性能的提升是AI爆发的重要基础