《计算之魂》 - 5 图论

概述：从几个图论问题开始

• 高效使用爬虫遍历所有网页，是有向连通图的遍历问题
• 广告和内容最大程度匹配
• 拼写自动矫正
• 服务器的连通性问题

5.1 图的本质：点与线

图的表示：

$$(V,E,\phi ,f)$$

• V 表示顶点，E 表示边，$\phi$表示顶点和边的映射关系，f 表示边的权重

历史：图论最早是莱昂哈德·欧拉研究的七桥问题。欧拉发明了只有点和线的抽象工具，可以解决平面图形问题和几何问题。

图的连通性和互联网之间关系：网络的出现导致信息交流的效率大大提升，就是因为互联网使得信息的连通信大大提升，信息传递的平均距离就越短。

相关算法问题：

• 关键路径问题
• 最大流问题
• 最短路径问题
• 最大匹配问题：N 个元素与 M 个元素之间的互相匹配问题，每个元素只能与对面的一个元素配对。这个问题可以表示为二分图问题。
• 博弈问题，例如下围棋的问题，白子黑子下棋问题（围棋棋盘的所有情况有$3^{361}$种）

最大匹配问题和博弈问题的相同点：

1. 节点的集合是有限的
2. 节点的关系是已经确定的（例如配对问题里总是 1:1 的关系，围棋问题里总是有下棋的先后顺序）
3. 两个节点之间的关系可以被量化度量

5.2 图遍历和连通

与树一样，图也可以用遍历算法遍历，得到图的生成树。

深度优先搜索

按照一个方向（顺时针、逆时针）遍历，如果这个方向已经遍历过了，就找下一个节点，最后生成一个比较深的树。

• 深度优先搜索算法较简单，使用语言的调用栈就可以实现

广度优先搜索

按照一层一层遍历图的节点，相比深度优先搜索，生成的是一个比较平衡的树。
伪代码（来自附录2）：

BFS(G, s) {  // G 为图，s 为起始点
    EnQueue(Q, s);
    while (Q not empty) {
        u = DeQueue(Q) // 取出一个节点
        u.tag = visited // 标记为访问
        for all v in u.Adjacent { // 访问 u 的周边节点
            if (v.tag == not_visited) { //如果没有访问过，则入队列
                EnQueue(Q, v);
            }
        } 
    }
}

例子

• 初始图

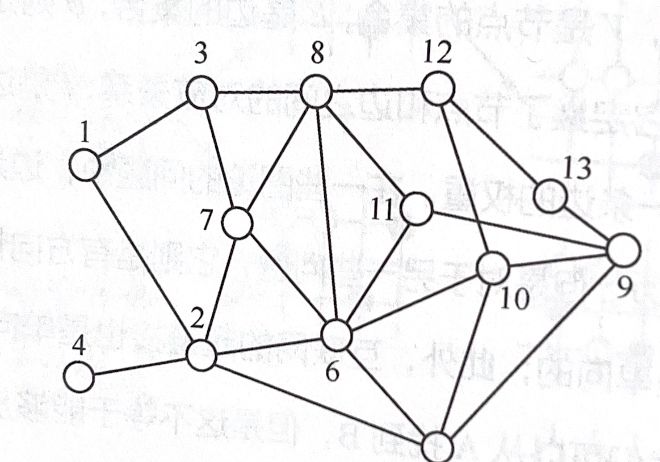
• 广度优先搜索结果

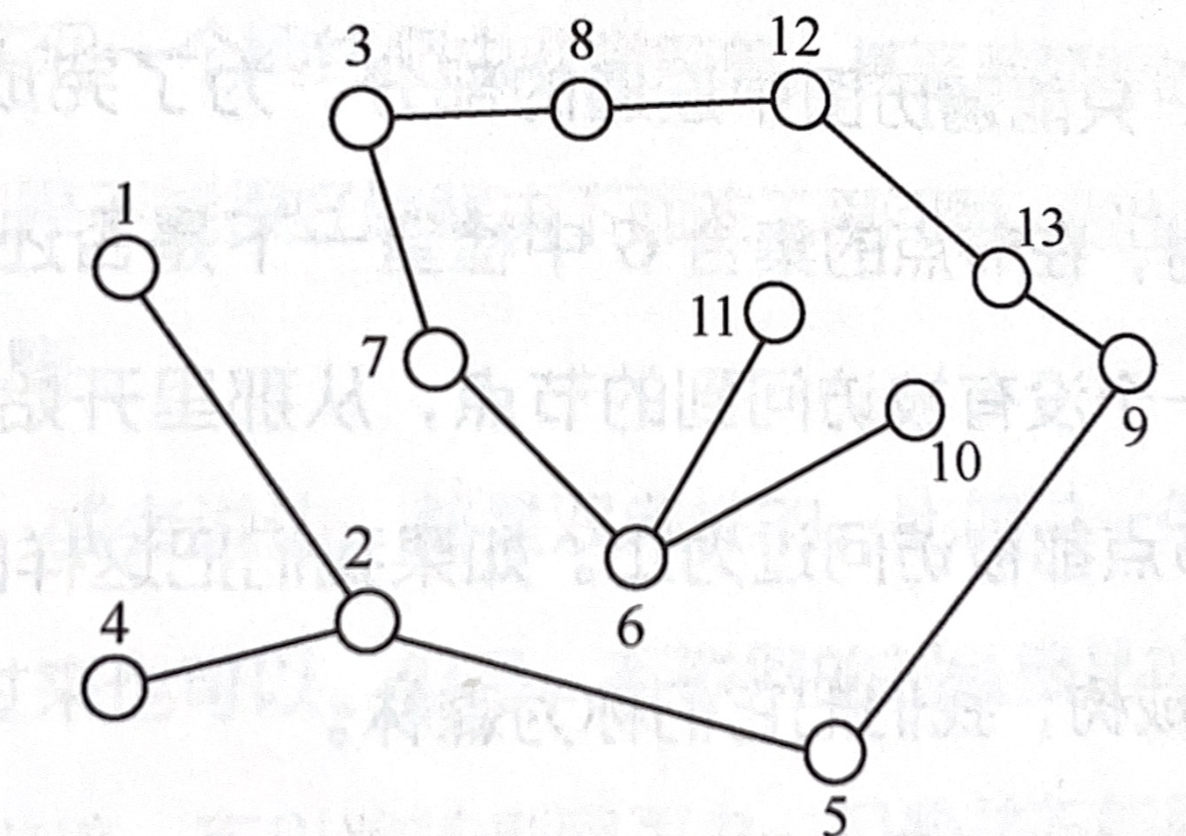
• 深度优先搜索结果

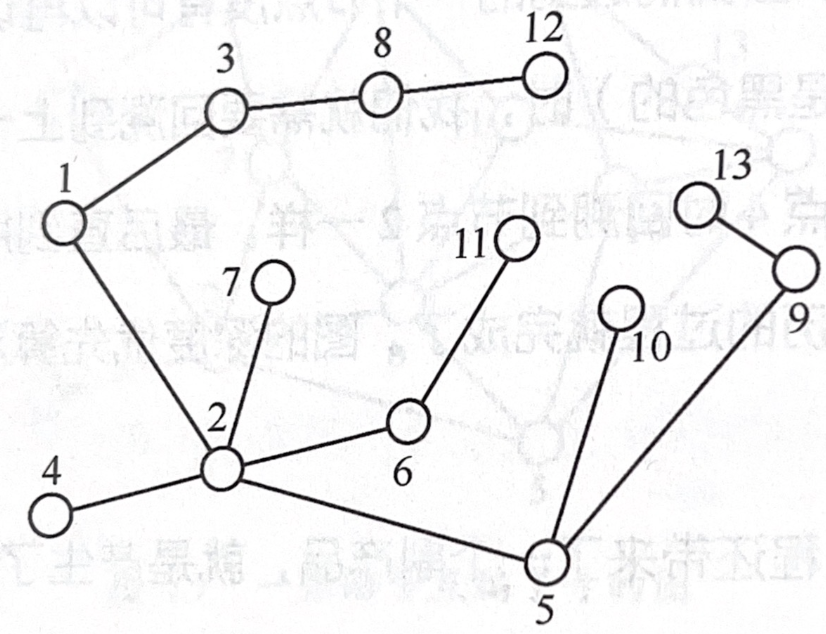
使用算法遍历只能遍历图中连通的部分，不连通的部分要人工调整访问。不连通的树组成的是一个森林。

5.3 网络爬虫的工程问题

• 图的有向性问题：网页的节点是单向的，而且未必所有的节点都是强连通的
• 节点的不可枚举问题：节点的总数量是不可知的，也不知道是否已经遍历了所有节点
• 节点和链接的动态变化：网页会更新，但是下载是有顺序的，很难保证下载下来的网页是最新的
• 体量问题：爬虫需要下载的量非常巨大，需要并行协调
• 并行协调：多服务器并行下载网页。构建两级爬虫系统，使用分布决策集中协调方法（一级服务器下载，一级服务器协调）
• 网速问题：如何在不影响网站服务的情况下，最快下载网页

5.4 动态规划算法

编辑距离问题：如何做一个自动矫正（英文）拼写错误的程序？

1. 计算字符串的差异：编辑距离

衡量两个字符串差异的参数值，满足三角不等式。

• 将字符串铺成一个二维网络，网络中的每个点可以向上、向右、向右上三个方向行进。其中向上和向右定义距离为1，向右上定义距离为0。

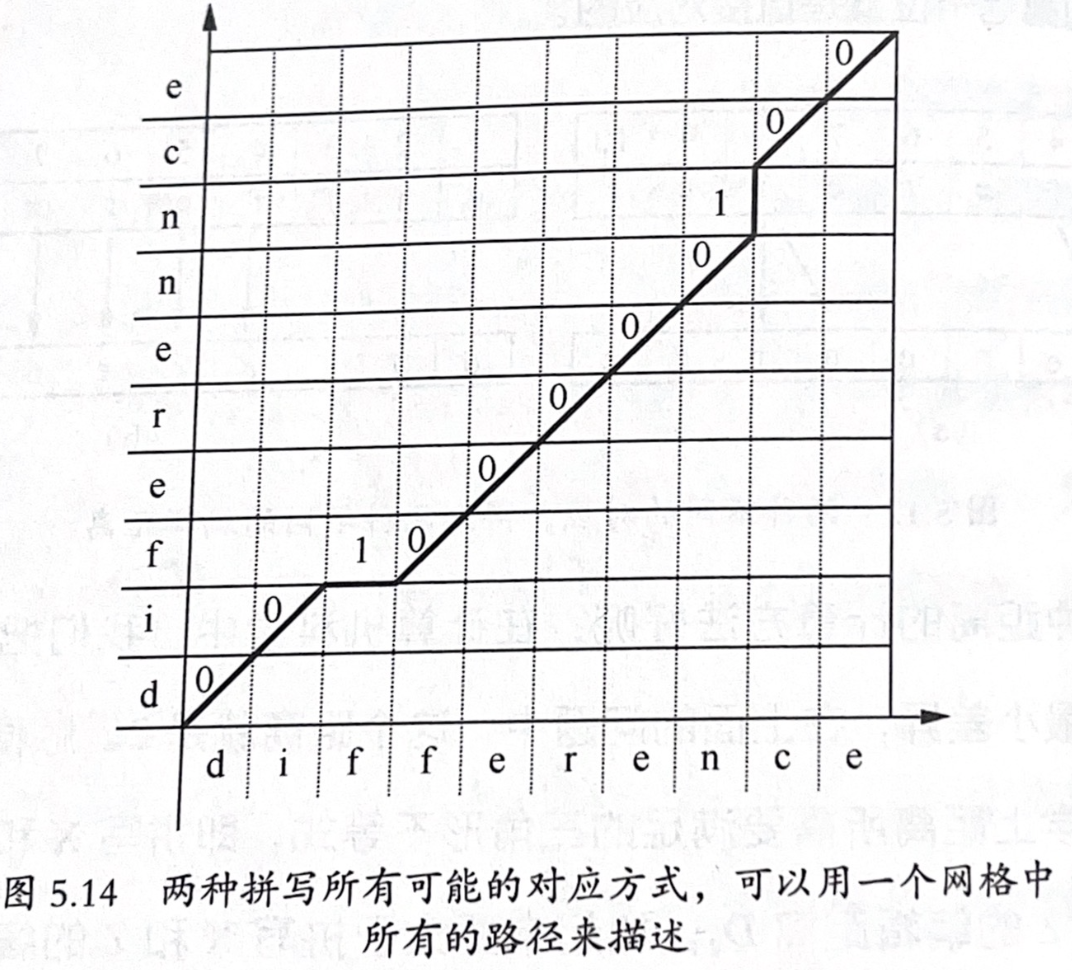
• 等效为最短路径问题：即为寻找一个从左下角到右上角代价最小的路径。

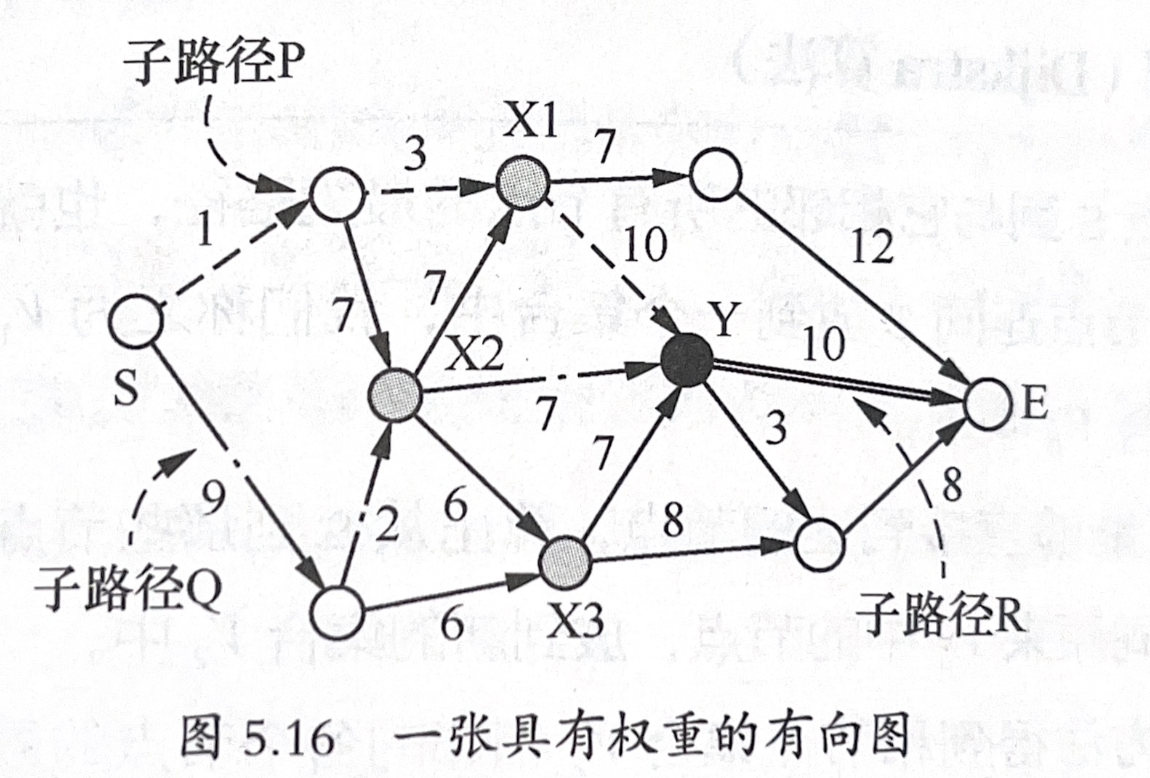
递归最短路径定理：如果某一路径在图中是最短的，那么这个路径中的子路径肯定是最短的。例如，已找出 S → E 的最短路径，那么其中经过的 S → Y 的路径也是最短的。

Dijkstra算法

基本步骤：

1. 找到起点 S，找 S 相邻节点做成最短路径，将以上所有节点放在集合 V1 中
2. 找到 V1 能够到达的所有节点，计算最短路径，放到新集合 V2 中
3. 最后直到找到最终节点 E

意义：将一个指数复杂度的问题简化为了$O(|V{|}^2+|E|)$复杂度。

局限性：

• 如果图中出现了负数回路，算法不可用（因为在回路中转圈可以减小路径最后输出的值）
• 可以加有向无环图的限制

代码（附录三 P206）：

• 队列作为基本数据结构，但书中代码有误（未将当前节点入队列，未检查相邻节点是否被访问过）

2. 找出出现概率最高的字符串

可以用统计的语言模型来解决。

工程细节

• 字母差距可以改为加权距离（在键盘上临近的字母可以设置较小的距离）
• 考虑打字时遇到的空格和字母写反的情况
• Dij 算法是一个加法算法，现实世界中很多问题是乘积关系（可以转换成对数问题解决）

思考题

1. 长方体嵌套问题
   • 思路：如果一个长方体可以嵌套在另一个长方体里，那么这个长方体的另两条边也可以嵌套，所以这是一个动态规划问题。
   • 回答参考：知乎
2. 主干网的建设问题
   • 思路：如果上半部分和下半部分节点同样多，主干网建设在任意一点的中间即可；否则偏向节点多的一侧。
   • 参考：知乎

5.5 最大流问题解决交通问题的方法

最大流：如何计算图中一个起始点到另一个点的最大流量？

• 最大流问题在云服务中常见（如带宽分配）

福特-富尔克森算法

算法主要步骤：

1. 分割：将一个图从起始点到结束点依次分割成两个子图，计算分割线上的通过流量，找到最小切割流量（即当前图的流量理论上限）
2. 增广：寻找一条从 S → T 上尚未饱和的路径（增广路径），增加流量，直到达到最小切割流量

局限性：

• 算法复杂度与最大边容量 F 正比（$O(|E|\cdot F)$），若 F 很大则收敛慢
• 改进版埃徳蒙兹-卡普算法复杂度为$O(|V||E{|}^2)$

伪代码（附录四 P207）：

Ford-Fulkerson(G, start, end) {
    while (Gr 中存在 start 到 end 的一条路径 path) {
        remaining(path) = min {remaining(u,v), (u,v) 在路径 path 上}
        for each (u,v) in path {
            if (flow(u,v) >= 0) {
                flow(u,v) += remaining(path);
            } else {
                flow(v,u) -= remaining(path);
            }
        }
    }
}

工程问题

1. QoS问题：流量的优先级不同
2. 流量的动态变化
3. 传输方向切换和改变的延时
4. 网络故障

思考题 5.4 增加光纤流量

1. 找新的最小切割流量
2. 将最小切割流量对应到饱和状态
3. 调整周边节点的进出流量
   参考：知乎

5.6 最大配对问题：二分图的最大流量问题

在二分图中寻找最大配对（使生成的配对包含的节点数量最多）。

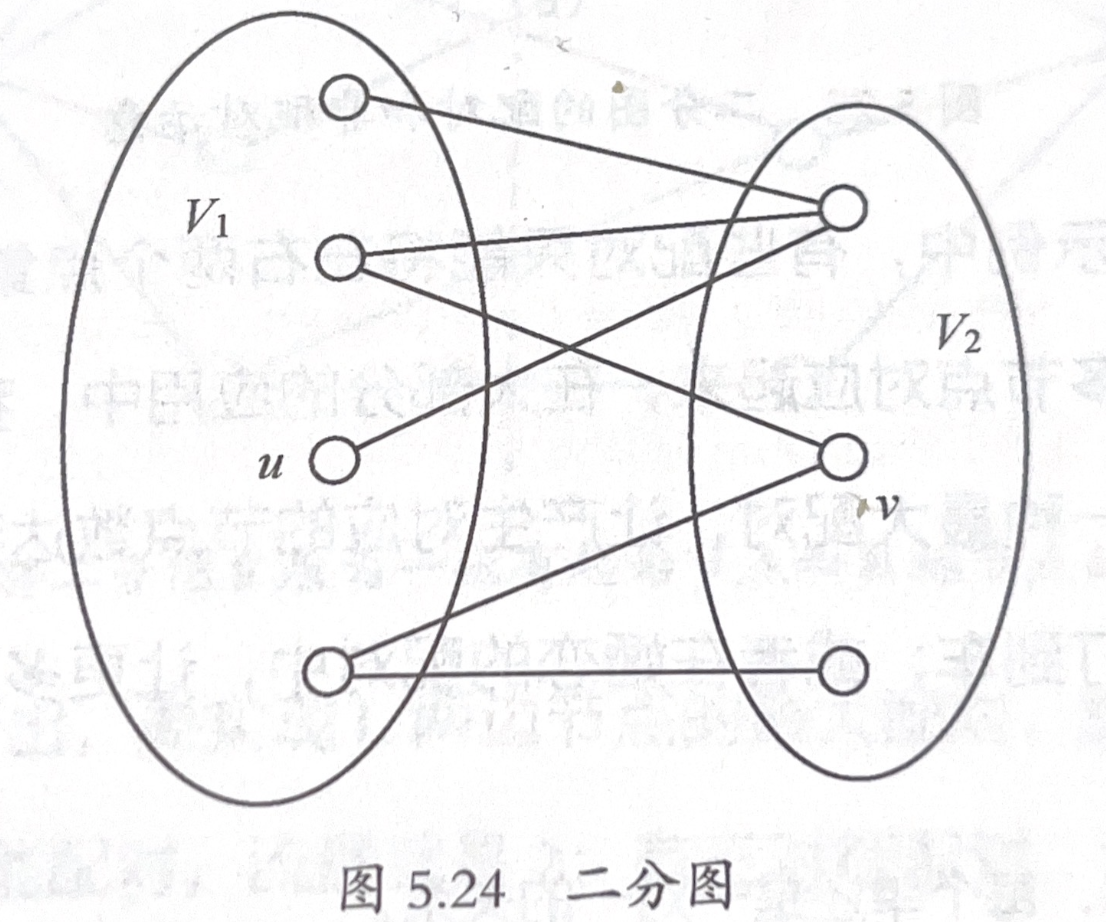
解决方法：

• 在二分图的左边构造起始节点 S，右边构造目标节点 T，形成新图。

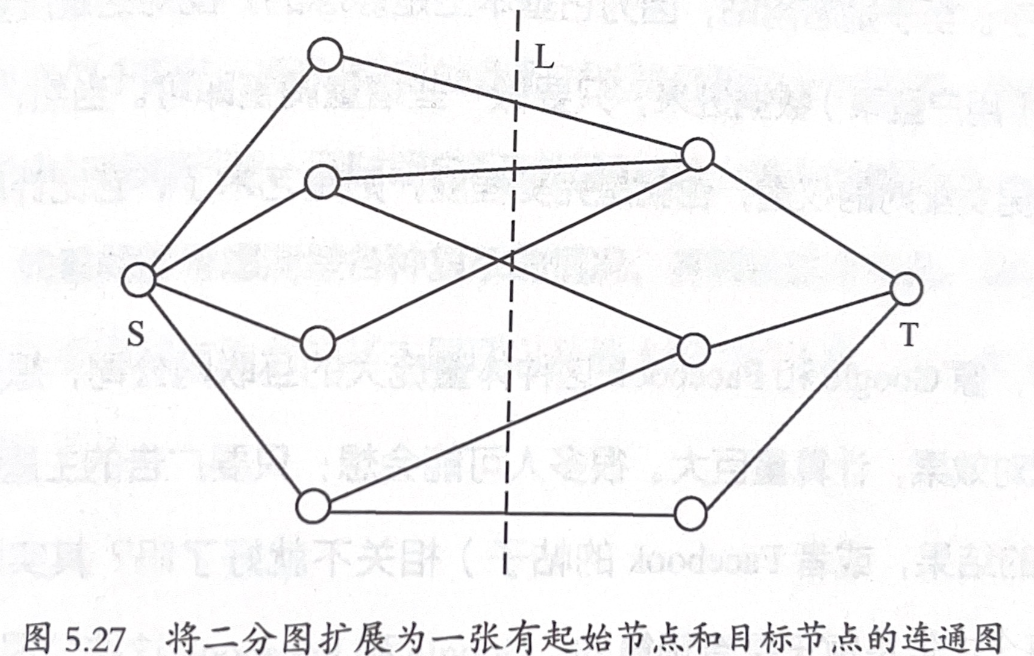
• 使用福特-富尔克森算法计算 S → T 的最大流。

工程应用

• 广告栏位和广告主的配对
• 网约车的动态配对
• 婚恋配对

思考题

1. 简历投递问题（M 个简历，N 个部门，每个简历投 k 部门，每个部门接受 d 简历）
   • 解决：设置 S 到求职者的流量为 k，部门到 T 的流量为 d，转化为最大流问题。
2. 简历与部门有 0-1 匹配度问题
   • 解决：在求职者到部门的路径上设置参数。
     参考：知乎