ref:
- e 自然常数,i 表示虚数
简化,当 时
理解
欧拉公式的左右两侧,都可以理解为在一个圆上的位置运动。
右侧:在复平面上的圆周运动
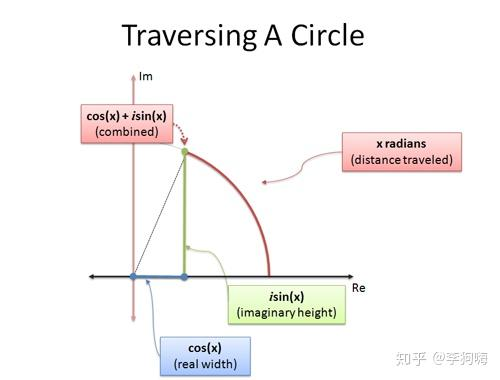
表示一个复数向量,向量指向一个圆周运动。
左侧
自然底数 e 的理解:在增长率为 100% 的连续复利的增值之后的最终结果。
增长概念:
- Q 总增长倍数
- rate 单位时间的增长率
- time 单位时间的数量
例如 表示增长率为 时的连续复利增长,在单位时间为 1 之后为增长 3 倍。
复平面的增长:
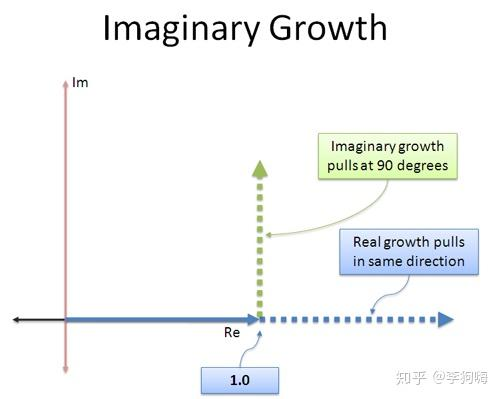
- 实数轴上的增长为当前向量方向的增长
- 虚数轴上的增长永远为 90 度方向上的增长
虚数的复平面的增长:
所以,在复平面的增长中,始终可以看成将复平面向量在 90 度方向上的转向变化。
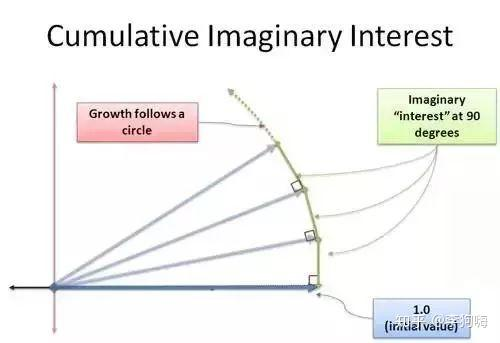
- 虚部的方向为实部的 90 度垂直夹角方向
- 因为这是一个 的极限问题,所以可以看作是实部的长度为定长,虚部的增长即为向量在 90 度方向上的持续转动
将自然底数加入复数指数时,得到
复数模长:实部和虚部的平方根 转向角度:虚部除以实部的 arctan
令 n 趋近于无穷,就得到模长的增长率为 1 ,角度增量为 1/n ,最终角度为 1,表示为 1 弧度的向量偏转。
得到:
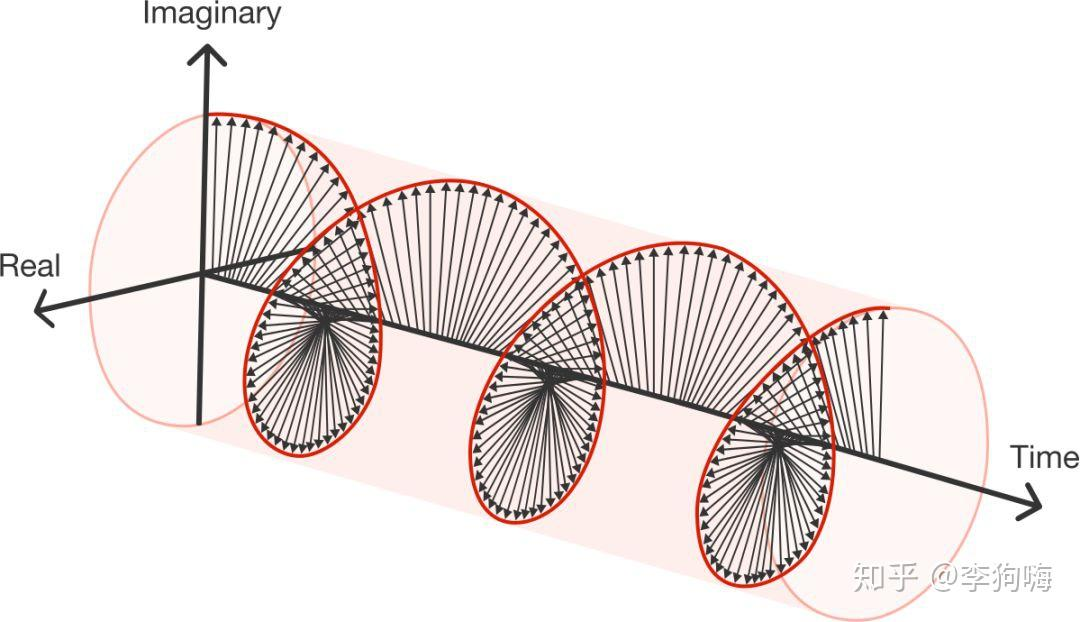
如果在时间轴上的呈现,即为: